
【题目】如图,在平面直角坐标系中有一正方形AOBC,反比例函数![]() 过正方形AOBC对角线的交点,半径为(
过正方形AOBC对角线的交点,半径为(![]() )的圆内切于△ABC,则k的值为______。
)的圆内切于△ABC,则k的值为______。

【答案】4
【解析】试题解析:设正方形对角线交点为D,过点D作DM⊥AO于点M,DN⊥BO于点N;
设圆心为Q,切点为H、E,连接QH、QE.

∵在正方形AOBC中,反比例函数y=![]() 经过正方形AOBC对角线的交点,
经过正方形AOBC对角线的交点,
∴AD=BD=DO=CD,NO=DN,HQ=QE,HC=CE,
QH⊥AC,QE⊥BC,∠ACB=90°,
∴四边形HQEC是正方形,
∵半径为(4-2![]() )的圆内切于△ABC,
)的圆内切于△ABC,
∴DO=CD,
∵HQ2+HC2=QC2,
∴2HQ2=QC2=2×(4-2![]() )2,
)2,
∴QC2=48-32![]() =(4
=(4![]() -4)2,
-4)2,
∴QC=4![]() -4,
-4,
∴CD=4![]() -4+(4-2
-4+(4-2![]() )=2
)=2![]() ,
,
∴DO=2![]() ,
,
∵NO2+DN2=DO2=(2![]() )2=8,
)2=8,
∴2NO2=8,
∴NO2=4,
∴DN×NO=4,
即:xy=k=4.


科目:初中数学 来源: 题型:
【题目】如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则: 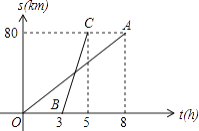
(1)摩托车每小时走千米,自行车每小时走千米;
(2)自行车出发后多少小时,它们相遇?
(3)摩托车出发后多少小时,他们相距10千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38 ①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39 ②,
②一①得:3S―S=39-1,即2S=39-1,
∴S=![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于直线l:y=kx+k(k≠0),下列说法不正确的是( )
A.点(0,k)在l上
B.l经过定点(﹣1,0)
C.当k>0时,y随x的增大而增大
D.l经过第一、二、三象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“国庆节”和“中秋节”双节期间,某微信群规定,群内的每个人都要发一个红包,并保证群内其他人都能抢到且自己不能抢自己发的红包,若此次抢红包活动,群内所有人共收到90个红包,则该群一共有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
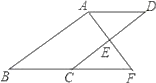
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,l1反映了甲离开A地的时间与离A地的距离的关系l2反映了乙离开A地的时间与离开A地距离之间的关系,根据图象填空: 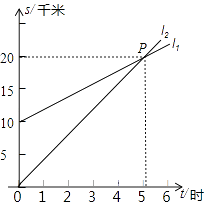
(1)当时间为0时,甲离A地千米;
(2)当时间为时,甲、乙两人离A地距离相等;
(3)图中P点的坐标是;
(4)l1对应的函数表达式是:S1=;
(5)当t=2时,甲离A地的距离是千米;
(6)当S=28时,乙离开A地的时间是时.
查看答案和解析>>
科目:初中数学 来源: 题型:
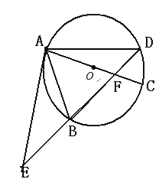
【题目】(本题满分8分)如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,
∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)在(2)的条件下,已知AF=4,CF=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表(图1)和频数分布直方图(图2).

请根据图表提供的信息,解答下列问题:
(1)表中的a= ,b= (2)请补全频数分布直方图;
(3)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应的圆心角的度数是 ;
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访,则正好抽到一名男同学和一名女同学的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com