
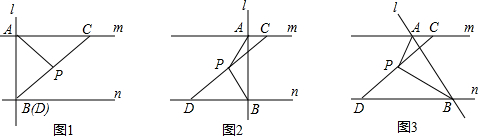
���� ��1������������CBD��ֱ�������Σ����ҵ�PΪ�߶�CD���е㣬Ӧ��ֱ�������ε����ʣ��ɵ�PA=PB���ݴ˽�ɣ�
��2��PA=PB��Ȼ�������ⷨһ����ͼ2���ӳ�AP��ֱ��n�ڵ�E��ֻҪ֤��PA=PE���ɣ��ⷨ������ͼ2-1����ֱ��l����ƽ�Ƶ�������P��λ�ã���AF=BE��ֻҪ֤����PAF�ա�PBE���ɣ��ⷨ������ͼ2-2����ֱ��l����ƽ�Ƶ�������C��λ�ã���AC=BE��ֻҪ֤����PAC�ա�PBE���ɣ�
��3���ⷨһ����ͼ3���ӳ�AP��ֱ��n�ڵ�E����AF��ֱ��n�ڵ�F��ֻҪ֤����AEF�ס�BEP���ɵ�$\frac{AE}{BE}$=$\frac{AF}{BP}$���Ƴ�AE•BP=AF•BE����AF=2k��AE=2PA��BE=AB���Ƴ�2PA•PB=2k•AB���ɵ�PA•PB=•AB��
�ⷨ������ͼ3-1�У��ӳ�AP��ֱ��n�ڵ�E����PH��m�ڵ�H����ֱ��n�ڵ�F��ֻҪ֤����AHP�ס�APB���ɣ��ⷨ������ͼ3-2�У��ӳ�AP��ֱ��n�ڵ�E����PH��m�ڵ�H����ֱ��n�ڵ�F����S��PAB=S��PEB����$\frac{1}{2}$•PA•PB=$\frac{1}{2}$BE•PF���ɴ˼��ɽ�����⣻
��� �⣺��1����ͼ1�У�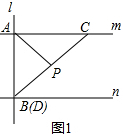
��l��m��
���BAC=90��
�֡ߵ�PΪ�߶�CD���е㣬
��PA=$\frac{1}{2}$CD=PB��
�ʴ�ΪPA=PB��
��2����ʱPA��PB�Ĺ�ϵʽ��Ȼ������֤�����£�
��ͼ2���ӳ�AP��ֱ��n�ڵ�E��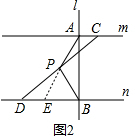
��m��n��
���ACP=��PDE����CAP=��PED��
�֡�PC=PD��
���PAC�ա�PED��AAS��
��PA=PE������P��AE���е㣬
�֡ߡ�ABE=90�㣬
��PA=PB��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룩��
�ⷨ������ͼ2-1����ֱ��l����ƽ�Ƶ�������P��λ�ã���AF=BE��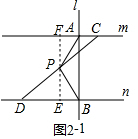
��m��n��
��$\frac{PC}{PD}$=$\frac{PF}{PE}$��
��PC=PD��
��PF=PE��
�ߡ�AFP=��BE=90�㣬
���PAF�ա�PBE��SAS����
��PA=PB��
�ⷨ������ͼ2-2����ֱ��l����ƽ�Ƶ�������C��λ�ã���AC=BE��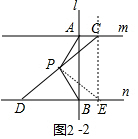
�ߡ�CED=90�㣬PC=PD��
��PC=PE��ֱ��������б���ϵ����ߵ���б�ߵ�һ�룩��
���PCE=��PEC��
��90��-��PCE=90��-��PEC������ACP=��BEP��
���PAC�ա�PBE��SAS����
��PA=PB��
��3���ⷨһ����ͼ3���ӳ�AP��ֱ��n�ڵ�E����AF��ֱ��n�ڵ�F��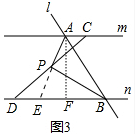
�ɣ�2����PA=PE��
�֡ߡ�APB=90�㣬
��BP���߶�AE�Ĵ�ֱƽ�֣�
��AB=BE��
�ߡ�AFE=��BPE=90�㣬��AEF=��BEP��
���AEF�ס�BEP��
��$\frac{AE}{BE}$=$\frac{AF}{BP}$��
��AE•BP=AF•BE��
��AF=2k��AE=2PA��BE=AB��
��2PA•PB=2k•AB��
��PA•PB=•AB��
�ⷨ������ͼ3-1�У��ӳ�AP��ֱ��n�ڵ�E����PH��m�ڵ�H����ֱ��n�ڵ�F��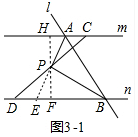
���PHA=90�㣮
��m��n��
��$\frac{PH}{PF}$=$\frac{PC}{DP}$��
��PC=PD��HF=k��
��PH=PF=k��
�ɣ�2����PA=PE��
�ߡ�APB=90�㣬��BP��AE��
��BP���߶�AE�Ĵ�ֱƽ�֣�
��AB=BE��
���AEB=��BAP��
��m��n��
���AEB=��HAP��
���BAP=��HAP��
�ߡ�PHA=��APB=90�㣬
���AHP�ס�APB��
��$\frac{PA}{AB}$=$\frac{PH}{PB}$��
��PA•PB=PH•AB����PA•PB=k•AB��
�ⷨ������ͼ3-2�У��ӳ�AP��ֱ��n�ڵ�E����PH��m�ڵ�H����ֱ��n�ڵ�F��
���PHA=90�㣮
��m��n��
��$\frac{PH}{PF}$=$\frac{PA}{PE}$=$\frac{PC}{PD}$��
��PC=PD��HF=2k��
��PA=PE��PH=PF=k��
�ɣ�2����PA=PE��
�ߡ�APB=90�㣬��BP��AE��
��BP���߶�AE�Ĵ�ֱƽ�֣�
��AB=BE��
��PA=PE��
��S��PAB=S��PEB����$\frac{1}{2}$•PA•PB=$\frac{1}{2}$BE•PF��
��PA•PB=kAB��
���� ���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ�ƽ���߷��߶γɱ���������֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ��������������λ�ȫ�������ν�����⣬֤�������Ƚ϶࣬�����п��������ͣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
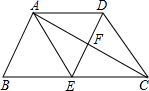 �ı���ABCD�У�AD��BC��DE��AC����BAC=90�㣬E��BC���е㣬�ı���AECD�����Σ�
�ı���ABCD�У�AD��BC��DE��AC����BAC=90�㣬E��BC���е㣬�ı���AECD�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
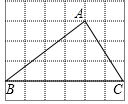 ��ͼ������ͼ�е�ÿ��С�����εı߳�����1����ABCÿ�����㶼�ڸ���ϣ���cosB=$\frac{4}{5}$��
��ͼ������ͼ�е�ÿ��С�����εı߳�����1����ABCÿ�����㶼�ڸ���ϣ���cosB=$\frac{4}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
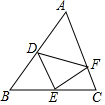 ��ͼ�����ABC�����Ϊ1����D��E��F�ֱ���AB��BC��CA�ϣ�AD=$\frac{1}{m}$AB��BE=$\frac{1}{n}$BC��CF=$\frac{1}{p}$CA��������m+n+p=9��m2+n2+p2=29��m3+n3+p3=99�����DEF�������
��ͼ�����ABC�����Ϊ1����D��E��F�ֱ���AB��BC��CA�ϣ�AD=$\frac{1}{m}$AB��BE=$\frac{1}{n}$BC��CF=$\frac{1}{p}$CA��������m+n+p=9��m2+n2+p2=29��m3+n3+p3=99�����DEF��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\overrightarrow{a}$+��-$\overrightarrow{a}$��=0 | B�� | $\overrightarrow{a}$+$\overrightarrow{0}$=-$\overrightarrow{a}$ | C�� | $\overrightarrow{0}$+��-$\overrightarrow{a}$��=$\overrightarrow{a}$ | D�� | |$\overrightarrow{0}$|=0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.765��105 | B�� | 7.65��104 | C�� | 76.5��103 | D�� | 7.65��105 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com