
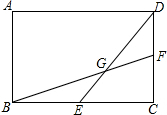
 如图,E、F分别是矩形ABCD的边AB、BC的中点,连接CE、AF,设CE、AF相交于点G,则S四边形ABGD:S四边形ABCD=2:3.
如图,E、F分别是矩形ABCD的边AB、BC的中点,连接CE、AF,设CE、AF相交于点G,则S四边形ABGD:S四边形ABCD=2:3. 分析 连接CG,BD,设S△BGE为S1,S△EGC为S2,S△GCF为S3,S△DGF为S4,S△BGC为S5.依题意可得S1+S2+S3=S2+S3+S4,得出S1=S4.由同底等高的三角形的面积相等得到S△ABF=S△BEC=$\frac{1}{4}$S矩形ABCD,由三角形的面积和得出S1+S2+S3=S4+S5.同理可得S2+S3+S4=S4+S5,由等量代换可得S1=S2,S3=S4,推出S1+S2+S3+S4+2S5=$\frac{1}{2}$S矩形ABCD,S1+S2+S3+S4=$\frac{2}{3}$×$\frac{1}{2}$.即可求得结果.
解答  解:连接CG,BD,
解:连接CG,BD,
设S△BGE为S1,S△EGC为S2,S△GCF为S3,S△DGF为S4,S△BGC为S5.
∵S△BCF=$\frac{1}{4}$S矩形ABCD=S△ECD,∴S1+S2+S3=S2+S3+S4,即S1=S4.
又∵S△BCFS△BFD=$\frac{1}{4}$S矩形ABCD,∴S1+S2+S3=S4+S5
同理,S2+S3+S4=S4+S5,而S1=S2,S3=S4.(等底同高)
∴S1+S2+S3+S4+2S5=$\frac{1}{2}$S矩形ABCD.
∴S1+S2+S3+S4=$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{3}$S矩形ABCD
∴S四边形ABGD:S矩形ABCD=(3-1):3=2:3,
故答案为:2:3.
点评 本题主要考查了矩形的性质以及三角形面积的计算问题,应熟练掌握.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:填空题
| 人数 | 平均身高(单位:厘米) | 方差 | |
| 男生 | 15 | 175 | 36 |
| 女生 | 15 | 165 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
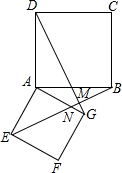 如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证:
如图,共顶点A的两个正方形ABCD、AEFG,连接DG、BE,且BE交DG于M点,交AG于N点.求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 5$\sqrt{5}$ | C. | 8 | D. | 10$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com