
【题目】如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数. 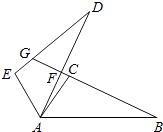
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】“互联网+”已全面进入人们的日常生活,据有关部门统计,目前全国4G用户数达到4.62亿,其中4.62亿用科学记数法表示为( )
A.4.62×104
B.4.62×106
C.4.62×108
D.0.462×108
查看答案和解析>>
科目:初中数学 来源: 题型:
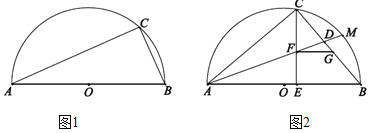
【题目】已知AB是半圆O的直径,点C在半圆O上.
(1)如图1,若AC=3,∠CAB=30°,求半圆O的半径;
(2)如图2,M是![]() 的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
的中点,E是直径AB上一点,AM分别交CE,BC于点F,D. 过点F作FG∥AB交边BC于点G,若△ACE与△CEB相似,请探究以点D为圆心,GB长为半径的⊙D与直线AC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一道题,已知线段AB=a,在直线AB上取一点C,使BC=b(a>b),点M,N分别是线段AB,BC的中点,求线段MN的长.对这道题,小善同学的答案是7,小昌同学的答案是3.老师说他们的结果都没错,如图,则依次可得到a的值是 . ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个学生方队,B的位置是第8列第7行,记为(8,7),则学生A在第二列第三行的位置可以表示为( )
A. (2,1) B. (3,3) C. (2,3) D. (3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:

设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一个例题:
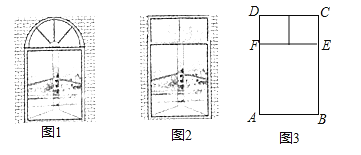
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:
(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com