阅读理解题:
我们知道一元二次方程是转化为一元一次方程来解的,例如:解方程x2-2x=0,通过因式分解将方程化为x(x-2)=0,从而得到x=0或x-2=0两个一元一次方程,通过解这两个一元一次方程,求得原方程的解.又如:解方程:x2-2x-3=0,通过配方,将方程化为(x-1)2-4=0,(x-1+2)(x-1-2)=0,即:(x+1)(x-3)=0,从而得到x+1=0或x-3=0两个一元一次方程,从而求得原方程的解.
请你仔细阅读上述内容,利用上述转化方法解下列一元二次不等式:
(1)2x(x-1)-3(x-1)<0;
(2)x2+6x+5>0.
【答案】
分析:(1)将不等式的左边分解因式得出(x-1)(2x-3)<0,根据有理数乘法法则得出两个不等式组,求出不等式组的解集,即可得出答案;
(2)将不等式的左边分解因式得出(x+1)(x+5)>0,根据有理数乘法法则得出两个不等式组,求出不等式组的解集,即可得出答案;
解答:解:(1)2x(x-1)-3(x-1)<0,
(x-1)(2x-3)<0,
即①
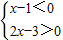
,②
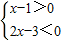
,
不等式组①的解集是空集;不等式组②的解集是:1<x<

,
即不等式2x(x-1)-3(x-1)<0的解集是:1<x<

.
(2)x
2+6x+5>0,
(x+1)(x+5)>0,
即①
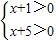
,②
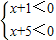
,
不等式组①的解集是x>-1,不等式组②的解集是x<-5,
即不等式x
2+6x+5>0的解集是x>-1或x<-5.
点评:本题考查了有理数的乘法法则和解一元一次不等式(组),关键是得出两个不等式组,题目比较好,但是有一定的难度.

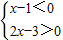 ,②
,②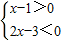 ,
, ,
, .
.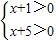 ,②
,②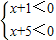 ,
,
