
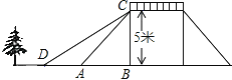
【题目】如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i= ![]() :3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:
:3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
【答案】不需要移栽,理由见解析
【解析】
根据题意得到三角形ABC为等腰直角三角形,求出AB的长,在直角三角形BCD中,根据新坡面的坡度求出∠BDC的度数为30,利用30度角所对的直角边等于斜边的一半求出DC的长,再利用勾股定理求出DB的长,由DB-AB求出AD的长,然后将AD+2与6进行比较,若大于则需要移栽,反之不需要移栽.
解:不需要移栽,理由为: ∵CB⊥AB,∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=5米,
在Rt△BCD中,新坡面DC的坡度为i= ![]() :3,即∠CDB=30°,
:3,即∠CDB=30°,
∴DC=2BC=10米,BD= ![]() BC=5
BC=5 ![]() 米,
米,
∴AD=BD﹣AB=(5 ![]() ﹣5)米≈3.66米,
﹣5)米≈3.66米,
∵2+3.66=5.66<6,
∴不需要移栽.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
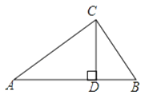
【题目】如图,在Rt△ABC中,∠C=90°,CD⊥AB于D.已知AB=13,CD=6,则Rt△ABC的周长为( )
A. 13+5![]() B. 13+13
B. 13+13![]() C. 13+9
C. 13+9![]() D. 18
D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲班56人,其中身高在160厘米以上的男同学10人,身高在160厘米以上的女同学3人,乙班80人,其中身高在160厘米以上的男同学20人,身高在160厘米以上的女同学8人.如果想在两个班的160厘米以上的女生中抽出一个作为旗手,在哪个班成功的机会大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
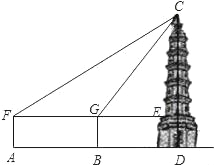
【题目】在一次数学活动课上,老师带领同学们区测量一座古塔CD的高度,他们首先在A处安置测量器,测得塔顶C的仰角∠CFE=30°,然后往塔的方向前进50米到达B处,此时测得塔顶C的仰角∠CGE=60°,已知测量器高1.5米,请你根据以上数据计算出古塔CD 的高度,(![]() ≈1.73,
≈1.73,![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:
当![]() ,
,![]() 时,
时,
![]() ,
,
![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
请利用上述结论解决以下问题:
(1)当![]() 时,
时,![]() 的最小值为__________.
的最小值为__________.
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
(3)请解答以下问题:
如图所示,某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成,设垂直于墙的一边长为![]() 米.若要围成面积为200平方米的花圃,需要用的篱笆最少是__________米.
米.若要围成面积为200平方米的花圃,需要用的篱笆最少是__________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80m的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为xm,矩形区域ABCD的面积为ym2.

(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)x为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com