
分析 分两种情形①如图1中,△ABC是锐角三角形时.②如图2中,△ABC是钝角三角形时,分别利用勾股定理,列出方程即可解决问题.
解答 解:如图1中,设AB=x,则CD=AB+BD=3+x,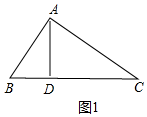
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AD2=AB2-BD2=AC2-CD2,
∴x2-32=(4$\sqrt{5}$)2-(x+3)2,
解得x=5或-8(舍弃),
∴BC=BD+CD=3+3+5=11.
如图2中,设AB=x,则CD=AB+BD=3+x,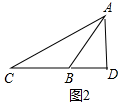
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴AD2=AB2-BD2=AC2-CD2,
∴x2-32=(4$\sqrt{5}$)2-(x+3)2,
解得x=5或-8(舍弃),
∴BC=CD-BD=5,
故答案为5或11.
点评 本题考查勾股定理的应用,解题的关键是学会用分类讨论的思想思考问题,注意有两种图形,学会构建方程解决问题,属于中考常考题型.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
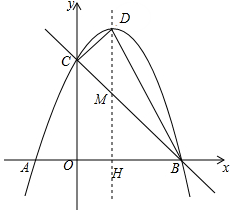 如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.
如图,已知抛物线y=-x2+bx+c轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于点P,与直线BC相交于点M,连接PB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP.
如图,已知矩形ABCD中,AB=4,AD=3,P是以CD为直径的半圆上的一个动点,连接BP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 苹果品种 | A | B | C |
| 每辆汽车装载量/吨 | 2.2 | 2.1 | 2 |
| 每吨苹果获利/元 | 600 | 800 | 500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com