
| �� �� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
| �����仯�����ˣ� | +0.5 | +0.7 | +0.8 | -0.4 | -0.6 | +0.2 | -0.1 |
���� ��1���Ƚ�ͳ�Ʊ��е����ݣ����ɵó������������������죬���ٵ������죬�Լ��������������ˣ�
��2������ƽ����ڼ�����������ٳ���300���������룮
��� �⣺��1��0.8-��-0.6��=1.4���ˣ�
���ο�������������3�գ����ٵ���5�գ����1.4���ˣ�
��2��0.5+0.7+0.8-0.4-0.6+0.2-0.1=1.1�����ˣ���
300����7��2+1.1��=4530����Ԫ����
���羰���ڴ�7����������Ϊ4530��Ԫ��
�ʴ�Ϊ��3��5��1.4��
���� ���⿼������������������ؼ���Ҫ������Ŀ����˼��������Ŀ��������������ʽ���㣬ע�ⵥλ��ͳһ��


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
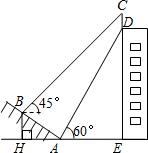 ��ͼ��ij��¥�Ķ�����һ������CD��С����ɽ�µ��½�A����ù���Ƶײ�D������Ϊ60�㣮������AB�����ߵ�B����ù���ƶ���C������Ϊ45�㣬��֪sin��BAH=$\frac{1}{2}$��AB=10�ף�AE=15�ף�
��ͼ��ij��¥�Ķ�����һ������CD��С����ɽ�µ��½�A����ù���Ƶײ�D������Ϊ60�㣮������AB�����ߵ�B����ù���ƶ���C������Ϊ45�㣬��֪sin��BAH=$\frac{1}{2}$��AB=10�ף�AE=15�ף��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com