
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
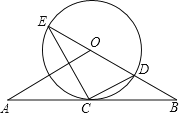
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
【答案】(1)见解析;(2)OA=5.
【解析】
(1)连接OC,通过等腰三角形中线的性质得出OC⊥AB,即可证明直线AB是⊙O的切线;
(2)通过证明△BCD∽△BEC,可得![]() ,设BD=x,则BC=2x,代入BC2=BDBE中,即可求得BD=2,根据OA=OB=BD+OD即可求出OA的长.
,设BD=x,则BC=2x,代入BC2=BDBE中,即可求得BD=2,根据OA=OB=BD+OD即可求出OA的长.
(1)证明:如图,连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB,
∴AB是⊙O的切线.
(2)解∵tan∠CED=![]() ,
,
∴![]() .
.
∵ED是直径,
∴∠ECD=90°,
∴∠E+∠EDC=90°.
又∵∠BCD+∠OCD=90°,∠OCD=∠ODC(OC=OD),
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△BCD∽△BEC.
∴![]() .
.
设BD=x,则BC=2x,
∵△BCD∽△BEC,
∴BC2=BDBE,
∴(2x)2=x(x+6).
∴x1=0,x2=2.
∵BD=x>0,
∴BD=2.
∴OA=OB=BD+OD=3+2=5.



 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有1个红球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回.大量重复该实验,发现摸到红球的频率稳定于0.25,求n的值.
(2)在(1)的条件下,从袋中随机摸出两个球,求两个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】纪中三鑫双语学校准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了m名学生(每名学生必选且只能选择这五项活动中的一种).

根据以上统计图提供的信息,请解答下列问题:
(1)m= ,n= .
(2)补全上图中的条形统计图.
(3)在抽查的m名学生中,有小薇、小燕、小红、小梅等10名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这4名女生中,选取2名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母A、B、C、D代表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D是AB边上的一点,连结CD,过点C作CD的垂线,与经过点C、D、B的圆交于点E,连结DE,交CB于点F.若AD=1,DB=3,则线段DE的长为_____;△CDF的面积为_____.
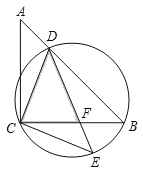
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“概率为0.0001的事件”是不可能事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“任意画出一个等边三角形,它是轴对称图形”是随机事件
D.“任意画出一个平行四边行,它是中心对称图形”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仿照例题完成任务:
例:如图1,在网格中,小正方形的边长均为![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 都在格点上,
都在格点上,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
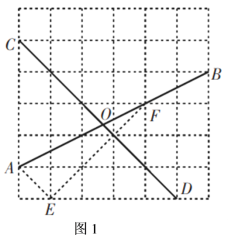
解析:连接![]() ,
,![]() ,导出
,导出![]() ,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
连接![]() ,
,![]() ,则
,则![]() ,
,
![]() ,根据勾股定理可得:
,根据勾股定理可得:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形,
是直角三角形,![]() ,
,
![]()
即![]() .
.
任务:
(1)如图2,![]() ,
,![]() ,
,![]() ,
,![]() 四点均在边长为
四点均在边长为![]() 的正方形网格的格点上,线段
的正方形网格的格点上,线段![]() ,
,![]() 相交于点
相交于点![]() ,求图中
,求图中![]() 的正切值;
的正切值;
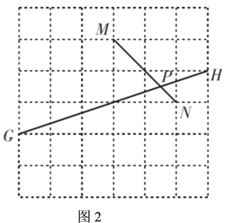
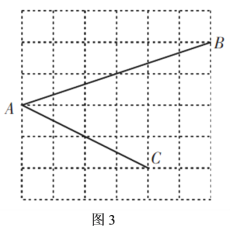
(2)如图3,![]() ,
,![]() ,
,![]() 均在边长为
均在边长为![]() 的正方形网格的格点上,请你直接写出
的正方形网格的格点上,请你直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在⊙O中,直径AB⊥弦CD于G,E为DC延长线上一点
(1)如图1,BE交⊙O于点F,求证:∠EFC=∠BFD;
(2)如图2,当CD也是直径,EF切⊙O于F,连接DF.若tan∠D=![]() ,求sin∠E的值.
,求sin∠E的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )
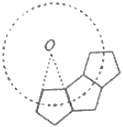
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连接CF并延长交AB于点M,MN⊥CM交射线AD于点N
(1)如图1,当点F为BE的中点时,求证:AM=CE;
(2)如图2,若![]() =
=![]() =n(n≥3)时,请直接写出
=n(n≥3)时,请直接写出![]() 的值;
的值;
(3)若矩形ABCD(AB>BC)对角线AC交MN于T,H为边BC上一点,∠CMH=45°且![]() =
=![]() (如图3).若CF平分∠ACB,请直接写出
(如图3).若CF平分∠ACB,请直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com