
【题目】长沙市马王堆蔬菜批发市场某批发商原计划以每千克10元的单价对外批发销售某种蔬菜![]() 为了加快销售,该批发商对价格进行两次下调后,售价降为每千克
为了加快销售,该批发商对价格进行两次下调后,售价降为每千克![]() 元.
元.
![]() 求平均每次下调的百分率;
求平均每次下调的百分率;
![]() 某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择
某大型超市准备到该批发商处购买2吨该蔬菜,因数量较多,该批发商决定再给予两种优惠方案以供选择![]() 方案一:打八折销售;方案二:不打折,每吨优惠现金1000元
方案一:打八折销售;方案二:不打折,每吨优惠现金1000元![]() 试问超市采购员选择哪种方案更优惠?请说明理由.
试问超市采购员选择哪种方案更优惠?请说明理由.
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
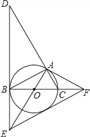
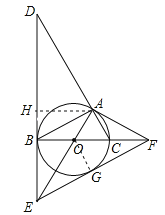
【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC=![]() ,求DE的长;
,求DE的长;
(3)连接EF,求证:EF是⊙O的切线.
【答案】(1) 见解析; (2)3![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;
(2)根据S△AOC=![]() ,得到S△ACF=
,得到S△ACF=![]() ,通过△ACF∽△DAE,求得S△DAE=
,通过△ACF∽△DAE,求得S△DAE=![]() ,过A作AH⊥DE于H,解直角三角形得到AH=
,过A作AH⊥DE于H,解直角三角形得到AH=![]() DH=
DH=![]() DE,由三角形的面积公式列方程即可得到结论;
DE,由三角形的面积公式列方程即可得到结论;
(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG=![]() (180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
(180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
试题解析:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°,∵∠ABC=30°,∴∠ACB=60°
∵OA=OC,∴∠AOC=60°,∵AF是⊙O的切线,∴∠OAF=90°,∴∠AFC=30°,∵DE是⊙O的切线,∴∠DBC=90°,∴∠D=∠AFC=30,∵∠DAE=ACF=120°,∴△ACF∽△DAE;
(2)∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,∴∠CAF=30°,∴∠CAF=∠AFC,∴AC=CF,∴OC=CF,∵S△AOC=![]() ,∴S△ACF=
,∴S△ACF=![]() ,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=
,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=![]() BD,∴AF=
BD,∴AF=![]() BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴
BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴![]() ,∵△ACF∽△DAE,∴
,∵△ACF∽△DAE,∴![]() =
=![]() ,∴S△DAE=
,∴S△DAE=![]() ,过A作AH⊥DE于H,∴AH=
,过A作AH⊥DE于H,∴AH=![]() DH=
DH=![]() DE,∴S△ADE=
DE,∴S△ADE=![]() DEAH=
DEAH=![]() ×
×![]()
![]() =
=![]() ,∴DE=
,∴DE=![]() ;
;
(3)∵∠EOF=∠AOB=120°,∴∠OEB=∠AFO,在△AOF与△BOE中,∵∠OBE=∠OAF,∠OEB=∠AFO,OA=OB,∴△AOF≌△BEO,∴OE=OF,∴∠OFG=![]() (180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
(180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
【题型】解答题
【结束】
25
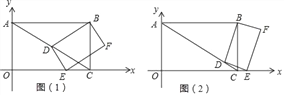
【题目】如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2![]() ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
(1)填空:点B的坐标为 ;
(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;
(3)①求证:![]() ;
;
②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瞳瞳做一道数学题:求代数式![]() 当x=-1时的值,由于瞳瞳粗心把式子中的某一项前的“+”号错误地看成了“—”号,算出代数式的值是-11,那么瞳瞳看错的是 次项前的符号,写出x=-1和x=1时代数式的值.
当x=-1时的值,由于瞳瞳粗心把式子中的某一项前的“+”号错误地看成了“—”号,算出代数式的值是-11,那么瞳瞳看错的是 次项前的符号,写出x=-1和x=1时代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扫黑除恶”受到广大人民的关注,某中学对部分学生就“扫黑除恶”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“很了解”部分所对应扇形的圆心角为_______;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对“扫黑除恶”知识达到“很了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
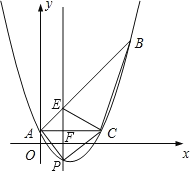
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),B(9,10),AC∥x轴,点P是直线AC下方抛物线上的动点。
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E.F,当四边形AECP的面积最大时,求点P的坐标和四边形AECP的最大面积;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C.P、Q为顶点的三角形与△ABC相似?若存在,求出点Q的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨地铁“二号线”正在进行修建,现有大量的残土需要运输.某车队有载重量为8吨、10吨的卡车共12台,全部车辆运输一次可以运输110吨残土.
(1)求该车队有载重量8吨、10吨的卡车各多少辆?
(2)随着工程的进展,该车队需要一次运输残土不低于165吨,为了完成任务,该车队准备再新购进这两种卡车共6辆,则最多购进载重量为8吨的卡车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是:购买10本以上,从第11本开始按标价的70%卖;乙商店的优惠条件是:每本按标价的80%卖.
(1)小明要买20本时,到哪个商店较省钱?
(2)买多少本时到两个商店付的钱一样?
(3)小明现有32元钱,最多可买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郴州市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买A、B两种奖品以鼓励抢答者.如果购买A种20件,B种15件,共需380元;如果购买A种15件,B种10件,共需280元.
(1)A、B两种奖品每件各多少元?
(2)现要购买A、B两种奖品共100件,总费用不超过900元,那么A种奖品最多购买多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com