
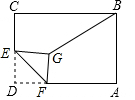
 如图,在矩形ABCD中,AB=2,BC=4,E是CD的中点,F是AD上的动点,将∠DEF沿EF所在的直线折叠,得到△D′EF,连接BD′,则BD′的最小值是$\sqrt{17}$-1.
如图,在矩形ABCD中,AB=2,BC=4,E是CD的中点,F是AD上的动点,将∠DEF沿EF所在的直线折叠,得到△D′EF,连接BD′,则BD′的最小值是$\sqrt{17}$-1. 分析 当∠BFE=∠B'EF,点B′在DE上时,此时B′D的值最小,根据勾股定理求出DE,根据折叠的性质可知B′E=BE=1,即可求出B′D.
解答 解:如图所示: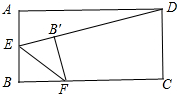 当∠BFE=∠B'EF,点B′在DE上时,此时B′D的值最小,
当∠BFE=∠B'EF,点B′在DE上时,此时B′D的值最小,
根据折叠的性质,△EBF≌△EB′F,
∴EB′⊥B′F,
∴EB′=EB,
∵E是AB边的中点,AB=2,
∴AE=EB′=1,
∵AD=BC=4,
∴DE=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$-1,
∴B′D=$\sqrt{17}$-1;
故答案为:$\sqrt{17}$-1.
点评 本题主要考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用;确定点B′在何位置时,B′D的值最小是解决问题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:选择题
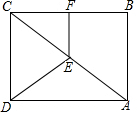 如图,E是矩形ABCD的对角线AC的中点,F是BC的中点,若AB=6,AD=8,则四边形CDEF的周长是( )
如图,E是矩形ABCD的对角线AC的中点,F是BC的中点,若AB=6,AD=8,则四边形CDEF的周长是( )| A. | 18 | B. | 19 | C. | 20 | D. | 23 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
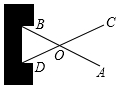 如图,把两根钢条AB,CD的中点O连在一起,可以做成一个测量工件内槽宽的工具(卡钳).只要量得AC之间的距离,就可知工件的内径BD.其数学原理是利用△AOC≌△BOD,判断△AOC≌△BOD的依据是( )
如图,把两根钢条AB,CD的中点O连在一起,可以做成一个测量工件内槽宽的工具(卡钳).只要量得AC之间的距离,就可知工件的内径BD.其数学原理是利用△AOC≌△BOD,判断△AOC≌△BOD的依据是( )| A. | SAS | B. | SSS | C. | ASA | D. | AAS |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com