
分析 先根据勾股定理得到a2=(b+1)2-b2=2b+1,而b是整数,b<2011,得到a2是1到4023之间的奇数,而且是完全平方数,32到632都这其中,所以a可以为3,5,…,63,由此得到满足条件的直角三角形的个数为31.
解答 解:∵两条直角边长分别是整数a,b(其中b<2011),斜边长是b+1,
∴a2=(b+1)2-b2=2b+1.
∴a2为奇数,
∵b是整数,b<2011,
∴a2是1到4023之间的奇数,而且是完全平方数,这样的数共有31个,即32,52,…,632.
∴a可以为3,5,…,63,
∴满足条件的直角三角形的个数为31.
故答案为:31.
点评 本题考查了完全平方数的概念.也考查了勾股定理以及会计算1~100的平方数.


科目:初中数学 来源: 题型:选择题
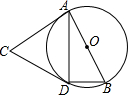 如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )
如图,AB是⊙O的直径,点C为⊙O外一点,CA、CD是⊙O的切线,A、D为切点,连接BD、AD.若∠ACD=48°,则∠DBA的大小是( )| A. | 48° | B. | 60° | C. | 66° | D. | 32° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李明同学要证明命题“三角形的中位线平行于三角形的第三边,并且等于第三边的一半”,他已经画出了图形,写出已知和求证,并请你帮助他写出证明过程.
李明同学要证明命题“三角形的中位线平行于三角形的第三边,并且等于第三边的一半”,他已经画出了图形,写出已知和求证,并请你帮助他写出证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连接AD,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.
已知:点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连接AD,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com