
(1)如图1,Rt△ABC中,∠B=90°,AB=2BC,现以C为圆心、CB长为半径画弧交边AC于D,再以A为圆心、AD为半径画弧交边AB于E.求证: .(这个比值
.(这个比值
叫做AE与AB的黄金比.)
(2)如果一等腰三角形的底边与腰的比等于黄金比,那么这个等腰三角形就叫做黄金三角形.请你以图2中的线段AB为腰,用直尺和圆规,作一个黄金三角形ABC.
(注:直尺没有刻度!作图不要求写作法,但要求保留作图痕迹,并对作图中涉及到的点用字母进行标注)
科目:初中数学 来源: 题型:解答题
如图,已知在△ABC中,AB=AC,BC比AB大3, ,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
,点G是△ABC的重心,AG的延长线交边BC于点D.过点G的直线分别交边AB于点P、交射线AC于点Q.
(1)求AG的长;
(2)当∠APQ=90º时,直线PG与边BC相交于点M.求 的值;
的值;
(3)当点Q在边AC上时,设BP= ,AQ=
,AQ= ,求
,求 关于
关于 的函数解析式,并写出它的定义域.[
的函数解析式,并写出它的定义域.[
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,方格纸中有一条美丽可爱的小金鱼.
(1)在同一方格纸中,画出将小金鱼图案绕原点O旋转180°后得到的图案;
(2)在同一方格纸中,并在 轴的右侧,将原小金鱼图案原点O为位似中心放大,使它们的位似比为1:2,画出放大后小金鱼的图案.
轴的右侧,将原小金鱼图案原点O为位似中心放大,使它们的位似比为1:2,画出放大后小金鱼的图案.
|

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,梯形 中,
中, ∥
∥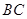 ,
, ,
, .一个动点
.一个动点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段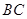 方向运动,过点
方向运动,过点 作
作 ,交折线段
,交折线段 于点
于点 ,以
,以 为边向右作正方形
为边向右作正方形 ,点
,点 在射线
在射线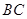 上,当
上,当 点到达
点到达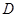 点时,运动结束.设点
点时,运动结束.设点 的运动时间为
的运动时间为 秒(
秒( ).
).
(1)当正方形 的边
的边 恰好经过点
恰好经过点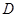 时,求运动时间
时,求运动时间 的值;
的值;
(2)在整个运动过程中,设正方形 与△
与△ 的重合部分面积为
的重合部分面积为 ,请直接写出
,请直接写出 与
与 之间的函数关系式和相应的自变量
之间的函数关系式和相应的自变量 的取值范围;
的取值范围;
(3)如图2,当点 在线段
在线段 上运动时,线段
上运动时,线段 与对角线
与对角线 交于点
交于点 ,将△
,将△ 沿
沿 翻折,得到△
翻折,得到△ ,连接
,连接 .是否存在这样的
.是否存在这样的 ,使△
,使△ 是等腰三角形?若存在,求出对应的
是等腰三角形?若存在,求出对应的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
数学课上,张老师出示图1和下面的条件:如图1,两个等腰直角三角板ABC和DEF有一条边在同一条直线l上,DE=2,AB=1.将直线EB绕点E逆时针旋转45°,交直线AD于点M.将图1中的三角板ABC沿直线l向右平移,设C、E两点间的距离为k.
解答问题:
(1)①当点C与点F重合时,如图2所示,可得 的值为 ;
的值为 ;
②在平移过程中, 的值为 (用含k的代数式表示);
的值为 (用含k的代数式表示);
(2)将图2中的三角板ABC绕点C逆时针旋转,原题中的其他条件保持不变.当点A落在线段DF上时,如图3所示,请补全图形,计算 的值;
的值;
(3)将图1中的三角板ABC绕点C逆时针旋转α度,0<α≤90,原题中的其他条件保持不变.计算 的值(用含k的代数式表示).
的值(用含k的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com