
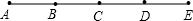


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源:数学教研室 题型:044
如图,A、O、B三点在一条直线上,∠AOE与∠BOE互为补角,用直尺和圆规分别画出∠AOE与∠BOE的平分线OC、OD,并说出图中共有几对互为余角的角,指出是哪几对?

查看答案和解析>>
科目:初中数学 来源: 题型:044
某小区内有A、B、C、D、E、F、G七个凉亭, 连结各个凉亭的几何平面图如图所示,其中AC=BC,∠ACB=90°,CD⊥AB,A、F、E在同一条直线上,C、F、G、D 也在同一条直线上。
现在我们来做一个“闯迷宫”的游戏,方法是:凉亭A为起点,凉亭B为终点,其中每经过一个凉亭可拿到一张纸片(每张纸片上的内容是:A处MN=M′N′;C处MH=M ′H′;E处∠M=∠M′;F处△MNH和△M′N′H′均为钝角三角形),其中凉亭C和F 之间有一水池不能直接到达.闯宫的规则是:当到达凉亭B处时,把你的纸片上的内容综合起来可以证明△MNH≌△M′N′H′才算走出迷宫.
请问:
(1)
共有几条路线可以走出迷宫(每两个凉亭之间不能重复走第二次, 图中实线表示人行道)?请写出来.(2)
哪一条路线行走的路程最短?
查看答案和解析>>
科目:初中数学 来源: 题型:044
如图,A、O、B三点在一条直线上,∠AOE与∠BOE互为补角,用直尺和圆规分别画出∠AOE与∠BOE的平分线OC、OD,并说出图中共有几对互为余角的角,指出是哪几对?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com