
分析 (1)用代入消元法求解即可;
(2)先求出两个不等式的解集,再求其公共解,然后写出整数解即可;
(3)方程组消去m得到关于x与y的方程,与x+y=12联立求出x与y的值,即可确定出m的值.
解答 解:$\left\{\begin{array}{l}{x=2y+3①}\\{3x=2y②}\end{array}\right.$,
把①代入②,得3(2y+3)=2y,
所以y=-$\frac{9}{4}$.
把y=-$\frac{9}{4}$代入①,得x=-$\frac{3}{2}$.
即原方程组的解为$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=-\frac{9}{4}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{x}{2}>-1①}\\{2x+1≥5(x-1)②}\end{array}\right.$
解不等式①得,x>-2,
解不等式②得,x≤2,
所以,不等式组的解集是-2<x≤2,
所以,不等式组的所有整数解是-10,1,2;
(3)$\left\{\begin{array}{l}{2x+3y=m①}\\{3x+5y=m+2②}\end{array}\right.$,
②-①得:x+2y=2,
与x+y=12联立得:$\left\{\begin{array}{l}{x+2y=2}\\{x+y=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=22}\\{y=-10}\end{array}\right.$,
则m=2x+3y=44-30=14.
点评 本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).也考查了二元一次方程组,熟练掌握运算法则是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
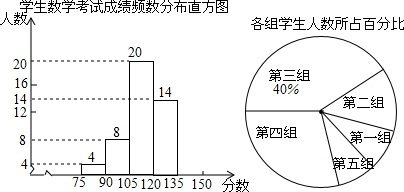
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
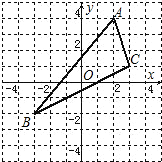 如图,△ABC中,A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(3,1).
如图,△ABC中,A点坐标为(2,4),B点坐标为(-3,-2),C点坐标为(3,1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 3 | C. | 4 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 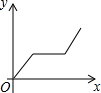 | B. | 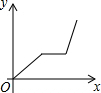 | C. | 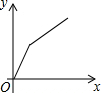 | D. | 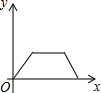 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
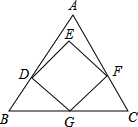 一个正方形和一个等边三角形的位置如图所示摆放,点G是BC中点,正方形对角线EG⊥BC,则∠AFE=( )
一个正方形和一个等边三角形的位置如图所示摆放,点G是BC中点,正方形对角线EG⊥BC,则∠AFE=( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com