
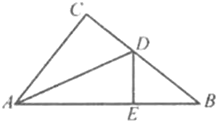
【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,DE⊥AB,垂足为E,若AC=3,AB=5,则DE的长为______.
【答案】![]()
【解析】
利用勾股定理求出BC的长,再利用角平分线的性质,易证CD=ED,利用HL证明Rt△ACD≌Rt△AED,根据全等三角形的对应边相等,可得AC=AE,即可求出BE的长,然后在Rt△BDE中,利用勾股定理求出DE的长.
解:在Rt△ABC中,![]() ,
,
∵AD平分∠CAB,DE⊥AB,∠ACB=90°,即AC⊥CB,
∴CD=DE,
在Rt△ACD和Rt△AED中,![]() ,
,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE=3,
∴BE=AB-AE=5-3=2,
设DE=CD=x,则BD=4-x,
在Rt△BDE中,BD2=DE2+BE2,
∴(4-x)2=x2+4,
解得:![]() ,
,
∴![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两家快递公司揽件员(揽收快件的员工)的日工资方案如下:
甲公司为“基本工资+揽件提成”,其中基本工资为70元/日,每揽收一件提成2元;
乙公司无基本工资,仅以揽件提成计算工资.若当日揽件数不超过40,每件提成4元;若当日搅件数超过40,超过部分每件多提成2元.
如图是今年四月份甲公司揽件员人均揽件数和乙公司搅件员人均揽件数的条形统计图:

(1)现从今年四月份的30天中随机抽取1天,求这一天甲公司揽件员人均揽件数超过40(不含40)的概率;
(2)根据以上信息,以今年四月份的数据为依据,并将各公司揽件员的人均揽件数视为该公司各揽件员的
揽件数,解决以下问题:
①估计甲公司各揽件员的日平均件数;
②小明拟到甲、乙两家公司中的一家应聘揽件员,如果仅从工资收入的角度考虑,请利用所学的统计知识帮他选择,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,CD、CM分别是斜边上的高和中线,那么下列结论中错误的是( )
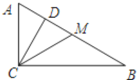
A.CM=ACB.∠ACM=∠DCBC.AD=DMD.DB=4AD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分线段AB.
(1)求∠A;
(2)若DE=2cm,BD=4cm,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小方格的边长为1,已知点A(2,2),把点A先向左平移4个单位,再向下平移2个单位到达点B;把点B先向右平移2个单位,再向下平移4个单位到达点C.

(1)在图中画出△ABC,并直接写出B,C两点的坐标:B( ),C( ).
(2)求△ABC的面积.
(3)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点![]() ,点
,点![]() 第1次向上跳动1个单位至点
第1次向上跳动1个单位至点![]() ,紧接着第2次向右跳动2个单位至点
,紧接着第2次向右跳动2个单位至点![]() ,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点
,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点![]() 第2019次跳动至点
第2019次跳动至点![]() 的坐标是( )
的坐标是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
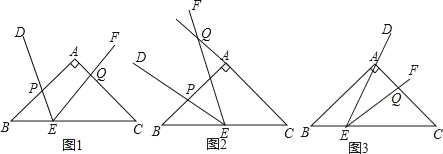
【题目】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.
(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;
(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的两个一元二次方程:
方程①:![]() ;
;
方程②:x2+(2k+1)x﹣2k﹣3=0.
(1)若方程①有两个相等的实数根,求:k的值
(2)若方程①和②只有一个方程有实数根,请说明此时哪个方程没有实数根.
(3)若方程①和②有一个公共根a,求代数式(a2+4a﹣2)k+3a2+5a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com