
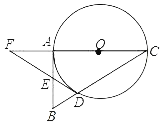
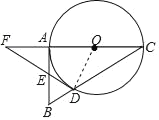
【题目】如图,在△ABC中,∠BAC=90°,以AC为直径的⊙O交BC于点D,点E在AB上,连接DE并延长交CA的延长线于点F,且∠AEF=2∠C.
(1)判断直线FD与⊙O的位置关系,并说明理由;
(2)若AE=2,EF=4,求⊙O的半径.
【答案】(1)直线FD与⊙O相切,理由详见解析;(2)⊙O的半径为2![]() .
.
【解析】
(1)连接OD,根据已知条件得到∠AEF=∠AOD,等量代换得到∠AOD+∠AED=180°,求得∠ODF=90°,于是得到结论;
(2)解直角三角形得到∠F=30°,AF=![]() ,求得OF=2OD,于是得到OD=FA,即可得到结论.
,求得OF=2OD,于是得到OD=FA,即可得到结论.
解:(1)直线FD与⊙O相切;
理由:连接OD,
∵∠AEF=2∠C,∠AOD=2∠C,
∴∠AEF=∠AOD,
∵∠AEF+∠AED=180°,
∴∠AOD+∠AED=180°,
∵∠BAC=90°,
∴∠ODF=90°,
∴直线FD与⊙O相切;
(2)∵∠BAC=90°,AE=2,EF=4,
∴∠F=30°,AF=![]() ,
,
∵∠ODF=90°,
∴OF=2OD,
∴OD=FA,
∴⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)求证:不论m为何值,该方程总有两个实数根;
(2)若直角△ABC的两直角边AB、AC的长是该方程的两个实数根,斜边BC的长为3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
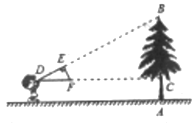
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高。
查看答案和解析>>
科目:初中数学 来源: 题型:
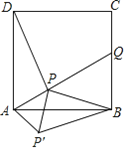
【题目】如图,点P是正方形ABCD内一点,连接AP并延长,交BC于点Q.连接DP.将△ADP绕点A顺时针旋转90°至△ABP'.连结PP',若AP=1,PB=2![]() ,PD=
,PD=![]() ,则正方形的边长为( )
,则正方形的边长为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是2019年4月份的日历,现用一长方形在日历表中任意框出4个数(如图2),下列表示a,b,c,d之间关系的式子中不正确的是( )

A. a﹣d=b﹣cB. a+c+2=b+dC. a+b+14=c+dD. a+d=b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加2018年的全国初中生数学竞赛,乔老师利用寒假把甲、乙两名同学的前五个学期的数学成绩(单位:分)统计成下表:
第一学期 | 第二学期 | 第三学期 | 第四学期 | 第五学期 | |
甲 | 75 | 80 | 85 | 90 | 95 |
乙 | 95 | 87 | 88 | 80 | 75 |
(1)分别求出甲、乙两名同学前五个学期的数学平均成绩;
(2)在图中分别画出甲、乙两名同学前五个学期的数学成绩的折线统计图;
(3)如果你是乔老师,你认为应该派哪名学生参加数学竞赛?请简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
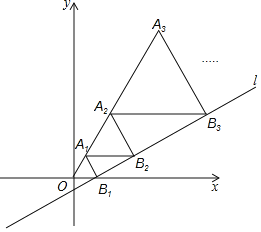
【题目】如图,在平面直角坐标系中,直线l:y=![]() 与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2019的横坐标是( )
与x轴交于点B1,以OB1为边长作等边三角形A1OB1,过点A1作A1B2平行于x轴,交直线于点B2,以A1B2为边长作等边三角形A2A1B2,过点A2作A2B3平行于x轴,交直线l于点B3,以A2B3为边长作等边三角形A3A2B3,…,则点A2019的横坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com