
【题目】如图,Rt△ABC中,∠C=90°,AB=5,AC=3,D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为( )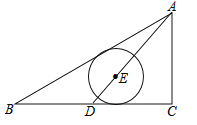
A.![]() ≤R≤
≤R≤![]()
B.![]() ≤R≤
≤R≤![]()
C.![]() ≤R≤2
≤R≤2
D.1≤R≤![]()
【答案】B
【解析】解:当点E在AD上,AD为△ABC的中线,如图1,作EH⊥BC于H,EF⊥AB于F,
∵以E为圆心的⊙E分别与AB、BC相切,
∴EH=EF=R,
在Rt△ABC中,∵∠C=90°,AB=5,AC=3,
∴BC=![]() =4,
=4,
∵点D为BC的中点,
∴BD=CD=2,
在Rt△ADC中,AD=![]() =
=![]() ,
,
∵EH∥AC,
∴△DEH∽△DAC,
∴![]() =
=![]() =
=![]() , 即
, 即![]() =
=![]() =
=![]() ,
,
∴DE=![]() R,DH=
R,DH=![]() R,
R,
∴AE=AD﹣DE=![]() ﹣
﹣![]() R,BH=BD+DH=2+
R,BH=BD+DH=2+![]() R,
R,
∵以E为圆心的⊙E分别与AB、BC相切,
∴BF=BH=2+![]() R
R
∴AF=AB﹣BF=3﹣![]() R,
R,
在Rt△AEF中,∵EF2+AF2=AE2 ,
∴R2+(3﹣![]() R)2=(
R)2=(![]() ﹣
﹣![]() R)2 , 解得R=
R)2 , 解得R=![]() ;
;
当点D运动到点C的位置,如图2,作EF⊥AB于F,
∵以E为圆心的⊙E分别与AB、BC相切,
∴EC=EF=R,
∴AE=AC﹣EC=3﹣R,
∵∠FAE=∠CAB,
∴Rt△AFE∽Rt△ACB,
∴![]() =
=![]() , 即
, 即![]() =
=![]() , 解得R=
, 解得R=![]() ,
,
∴当D点从BC的中点到C点运动,点E在AD上,以E为圆心的⊙E分别与AB、BC相切,则⊙E的半径R的取值范围为![]() ≤R≤
≤R≤![]() .
.
故选B.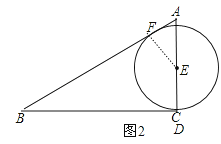
【考点精析】掌握切线的性质定理是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,CA=CB,AD是腰BC边上的高,△ACD的内切圆⊙E分别与边AD、BC相切于点F、G,连AE、BE.
(1)求证:AF=BG;
(2)过E点作EH⊥AB于H,试探索线段EH与线段AB的数量关系,并说明理由.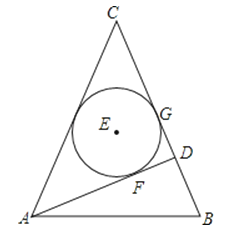
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上的位置如图所示,O为原点,现A,B两点分别以1个单位长度/秒的速度同时向左运动。
(1)几秒后,原点恰好在A,B两点正中间?
(2)几秒后,恰好有OA:OB=1:2.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-3pq)2;
(2)-x3+(-4x)2x;
(3)(m4m÷m2n)·mn;
(4)(-2)-2-32÷(3.144+π)0;
(5)(a2)3·(a2)4÷(-a2)5;
(6)[-2-3-8-1×(-1)-2]×![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O与直线l相切于A点,点P、Q同时从A点出发,P沿着直线l向右、Q沿着圆周按逆时针以相同的速度运动,当Q运动到点A时,点P也停止运动.连接OQ、OP(如图),则阴影部分面积S1、S2的大小关系是( )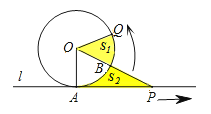
A.S1=S2
B.S1≤S2
C.S1≥S2
D.先S1<S2 , 再S1=S2 , 最后S1>S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,DB⊥AB,已知AC=2,AB=6,点P射线BD上一动点,以CP为直径作⊙O,点P运动时,若⊙O与线段AB有公共点,则BP最大值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )
(栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)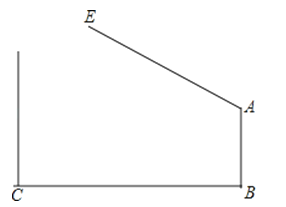
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=44°,∠BAD=28°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC= 度;
(2)求∠EDF的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com