
 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于第二、四象限内的A、B两点,与y轴交于C点,过A作AH⊥y轴于H,OH=3,tan∠AOH=$\frac{4}{3}$,点B的坐标为(m,-2).分析 (1)根据tan∠AOH=$\frac{4}{3}$求出AH的长度,由勾股定理可求出OH的长度即可求出△AHO的周长.
(2)根据点A的坐标为(-4,3),点A在反比例函数的图象上,可求出k的值,将点B的坐标代入反比例函数的解析式中求出m的值,然后将A、B两点的坐标代入一次函数解析式中即可求出该一次函数的解析式.
解答  解:(1)∵AH⊥y轴于点H,
解:(1)∵AH⊥y轴于点H,
∴∠AHO=90°,
∴tan∠AOH=$\frac{4}{3}$,AH=4,
∴OH=3,
∴由勾股定理可求出OA=5,
∴△AHO的周长为3+4+5=12;
(2)由(1)可知:点A的坐标为(-4,3),
把(-4,3)代入y=$\frac{k}{x}$,可得k=-12,
∴反比例函数的解析式为:y=-$\frac{12}{x}$,
∵把B(m,-2)代入反比例函数y=-$\frac{12}{x}$中,可得m=6,
∴点B的坐标为(6,-2),
将A(-4,3)和B(6,-2)代入y=ax+b,可得
$\left\{\begin{array}{l}{3=-4a+b}\\{-2=6a+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为:y=-$\frac{1}{2}$x+1.
点评 本题考查一次函数与反比例函数的综合问题,解题的关键是求出点A与B的坐标,运用待定系数法即可得到函数解析式.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
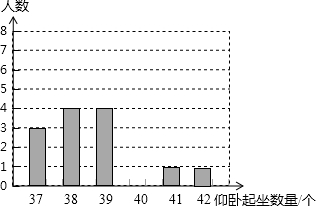 某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题| 测试成绩(个) | 学生数(名) | 百分比 |
| 37 | 3 | P% |
| 38 | 4 | 20% |
| 39 | 4 | 20% |
| 40 | N | 35% |
| 41 | 1 | 5% |
| 42 | 1 | 5% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线y1=-mx+5m与双曲线y2=$\frac{k}{x}$(x>0)相交于A、B(4,n)两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.
如图,直线y1=-mx+5m与双曲线y2=$\frac{k}{x}$(x>0)相交于A、B(4,n)两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间段(小时/周) | 小丽抽样(人数) | 小杰抽样(人数) |
| 0~1 | 6 | 22 |
| 1~2 | 10 | 10 |
| 2~3 | 16 | 6 |
| 3~4 | 8 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
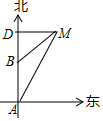 如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).
如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com