
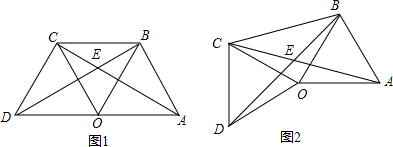
分析 (1)如图1,根据等边三角形的性质得到OD=OC=OA=OB,∠COD=∠AOB=60°,则利用根据“SAS”判断△AOC≌△BOD;
(2)利用△AOC≌△BOD得到∠CAO=∠DBO,然后根据三角形内角和可得到∠AEB=∠AOB=60°;
(3)如图2,与(1)的方法一样可证明△AOC≌△BOD;则∠CAO=∠DBO,然后根据三角形内角和可求出∠AEB=∠AOB=60°.
解答 (1)证明:如图1,
∵△ODC和△OAB都是等边三角形,
∴OD=OC=OA=OB,∠COD=∠AOB=60°,
∴∠BOD=∠AOC=120°,
在△AOC和△BOD中
$\left\{\begin{array}{l}{OC=OD}\\{∠AOC=∠BOD}\\{OA=OB}\end{array}\right.$
∴△AOC≌△BOD;
(2)解:∵△AOC≌△BOD,
∴∠CAO=∠DBO,
∵∠1=∠2,
∴∠AEB=∠AOB=60°;
(3)解:如图2,∵△ODC和△OAB都是等边三角形,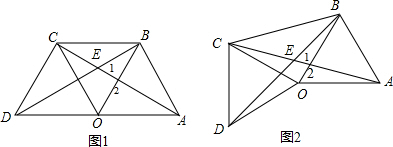
∴OD=OC=OA=OB,∠COD=∠AOB=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
在△AOC和△BOD中
$\left\{\begin{array}{l}{OC=OD}\\{∠AOC=∠BOD}\\{OA=OB}\end{array}\right.$
∴△AOC≌△BOD;
∴∠CAO=∠DBO,
∵∠1=∠2,
∴∠AEB=∠AOB=60°,
即∠AEB的大小不变.
故答案为不变.
点评 本题考查了几何变换综合题:熟练掌握旋转的性质、等边三角形的性质和全等三角形的判定与性质;利用类比的方法解决(3)小题.


科目:初中数学 来源: 题型:填空题
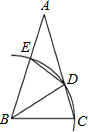 △ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为67.5°.
△ABC中,AB=AC,∠A=30°,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E两点,并连结BD,DE. 则∠BDE的度数为67.5°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
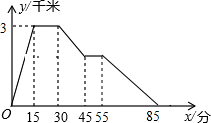 张强从家跑步去体育场,在那里锻炼了一阵后又到文具店买笔,然后散步回家.已知张强家、体育场、文具店在同一直线上,他从家跑步到体育场的平均速度是他从体育场到文具店的平均速度的2倍.设他出发后所用的时间为x(单位:min),离家的距离为y(单位:km),y与x的函数关系如图所示,则下列说法中错误的是( )
张强从家跑步去体育场,在那里锻炼了一阵后又到文具店买笔,然后散步回家.已知张强家、体育场、文具店在同一直线上,他从家跑步到体育场的平均速度是他从体育场到文具店的平均速度的2倍.设他出发后所用的时间为x(单位:min),离家的距离为y(单位:km),y与x的函数关系如图所示,则下列说法中错误的是( )| A. | 体育场离张强家的距离为3km | |
| B. | 体育场离文具店的距离为1.5km | |
| C. | 张强从体育场到文具店的平均速度为100m/min | |
| D. | 张强从文具店散步回家的平均速度为60m/min |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知等边△ABC的边长为8,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )
如图,已知等边△ABC的边长为8,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )| A. | 3 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com