
 有一个附有进水管的容器,每单位时间内进水量都是一定的,设从某时刻开始的4分钟内只进水、不出水,在随后的8分钟内既进水,又出水,得到时间x(分)与容器内水量y(升)之间的关系如图所示:
有一个附有进水管的容器,每单位时间内进水量都是一定的,设从某时刻开始的4分钟内只进水、不出水,在随后的8分钟内既进水,又出水,得到时间x(分)与容器内水量y(升)之间的关系如图所示: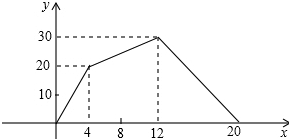 解:(1)4分钟时,进水20升;
解:(1)4分钟时,进水20升;| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |


科目:初中数学 来源: 题型:
 如图,已知B,C,D三点在一条直线上,AC⊥BD,DE⊥BD,AB⊥BE,
如图,已知B,C,D三点在一条直线上,AC⊥BD,DE⊥BD,AB⊥BE,| 7 |
| 8 |
| 7 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 甲、乙两车分别从相距360千米的A、B两地同时相向出发,甲车到B地休息1小时后返回A地时速度提高为原来的
甲、乙两车分别从相距360千米的A、B两地同时相向出发,甲车到B地休息1小时后返回A地时速度提高为原来的| 5 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间x | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)
如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com