
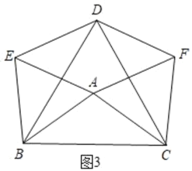
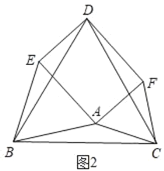
【题目】已知如图:分别以△ABC的各边为边,在BC边的同侧作等边三角形ABE、等边三角形CBD和等边三角形ACF,连结DE,DF.

(1)试说明四边形DEAF为平行四边形.
(2)当△ABC满足什么条件时,四边形DEAF为矩形?并说明理由;
(3)当△ABC满足什么条件时,四边形DEAF为菱形.直接写出答案 .
【答案】(1)见解析;(2)∠BAC=150°时,见解析;(3)![]() ,见解析.
,见解析.
【解析】
(1)根据等边三角形的性质得∠ABE=∠CBD=60°,AB=BE=AE,CB=BD=CD,则∠ABC=∠EBD,于是可利用“SAS”判断△ABC≌△EBD,得到AC=DE,再由△ACF为等边三角形得AC=AF,则AF=DE,同理可证△ACB≌△FCD得到AB=DF,则AE=DF,然后根据平行四边形的判定方法即可得到结论;
(2)由于四边形DEAF是平行四边形,当∠EAF=90°时,四边形DEAF为矩形,根据等边三角形角的大小,可得∠BAC=150°;
(3)由于四边形DEAF是平行四边形,根据菱形的判定方法,当AE=AF时,四边形DEAF是菱形,此时AB=AC.
解:(1)如图1,∵△ABE和△CBD为等边三角形,
∴∠ABE=∠CBD=60°,AB=BE=AE,CB=BD=CD,
∴∠ABC=∠EBD,
在△ABC和△EBD中,
 ,
,
∴△ABC≌△EBD(SAS),
∴AC=DE,
∵△ACF为等边三角形,
∴AC=AF,
∴AF=DE,
同理可证得△ACB≌△FCD,
∴AB=DF,
而AB=AE,
∴AE=DF,
∴四边形DEAF是平行四边形;
(2)如图2,当△ABC满足∠BAC=150°时,四边形DEAF是矩形.
理由如下:
由(1)知:四边形DEAF是平行四边形,
∵∠BAC=150°,∠EAB=∠FAC=60°
∴∠EAF=360°﹣150°﹣60°﹣60°=90°
∴四边形DEAF是矩形;
(3)如图3,△ABC满足AB=AC时,四边形DEAF是菱形.
理由如下:
由(1)知:四边形DEAF是平行四边形,
∵AB=AC,AE=AB,AC=AF,
∴AE=AF,
∴四边形DEAF是菱形.
故答案为:AB=AC.



科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
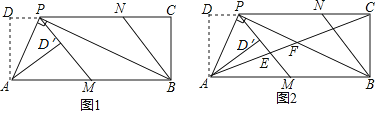
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC,分别交PM,PB于点E,F.若![]() =
=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,给出如下定义:若点P的横、纵坐标均为整数,且到圆心C的距离d≤r,则称P为⊙C 的关联整点.
(1)当⊙O的半径r=2时,在点D(2,-2),E(-1,0),F(0,2)中,为⊙O的关联整点的是 ;
(2)若直线![]() 上存在⊙O的关联整点,且不超过7个,求r的取值范围;
上存在⊙O的关联整点,且不超过7个,求r的取值范围;
(3)⊙C的圆心在x轴上,半径为2,若直线![]() 上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
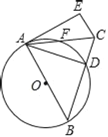
(1)求证:AD=AE.
(2)若AB=10,sin∠DAC=![]() 求AD的长.
求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解七年级学生体能状况,从七年级学生中随机抽取部分学生进行体能测试,测试结果分为A、B、C、D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图:
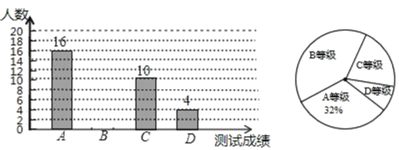
(1)这次抽样调查的样本容量是 ,请补全条形图;
(2)D等级学生人数占被调查人数的百分比为 ,在扇形统计图中B等级所对应的圆心角为 .
(3)该校九年级学生有1600人,请你估计其中A等级的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现实社会中,塑料袋仍然是白色污染的一部分,为了解塑料袋的使用情况,某校八年级环保小组随机抽取“幸福小区”40户居民家庭,记录了这些家庭某个月丢弃塑料袋的数量(单位:个)如下:
29 39 35 39 39 27 33 35 31 31
32 32 34 31 33 39 38 40 38 42
31 31 38 31 39 27 33 35 40 38
29 39 35 33 39 39 38 42 37 32
请根据上述数据,解答以下问题:
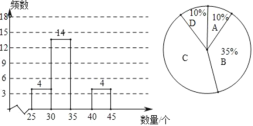
(1)若数据为x,按“组距为5”列出了如下的频数分布表,请将表中空缺的部分补充完整,并补全频数分布直方图;
分组 | 频数 |
A:25≤x<30 | 4 |
B:30≤x<35 | 14 |
C:35≤x<40 | |
D:40≤x<45 | 4 |
合计 | 40 |
(2)根据(1)中的直方图可以看出,这40户居民家庭这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,画出了如图所示的扇形统计图,请求出C组对应的扇形圆心角的度数;
(4)若该小区共有1000户居民家庭,请你估计每月丢弃的塑料袋数量不小于30个的家庭户数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min) 之间的函数关系如图所示.有下列说法: ①A、B之间的距离为1200m;②甲行走的速度是乙的1.5倍;③![]() ;④
;④![]() .以上结论正确的有( )
.以上结论正确的有( )
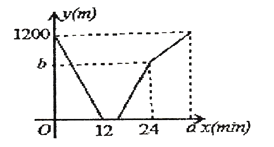
A.①④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2﹣![]() x+c交x轴于A,B两点,交y轴于点C.直线y=﹣
x+c交x轴于A,B两点,交y轴于点C.直线y=﹣![]() x+3经过点B,C.
x+3经过点B,C.
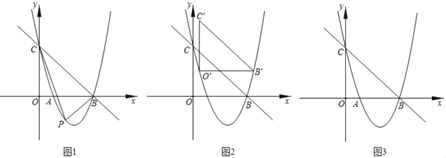
(1)求抛物线的解析式;
(2)若点P为直线BC下方的抛物线上一动点(不与点B,C重合),则△PBC的面积能够等于△BOC的面积吗?若能,求出相应的点P的坐标;若不能,请说明理由;
(3)如图2,现把△BOC平移至如图所示的位置,此时三角形水平方向一边的两个端点点O′与点B′都在抛物线上,称点O′和点B′为△BOC在抛物线上的一“卡点对”;如果把△BOC旋转一定角度,使得其余边位于水平方向然后平移,能够得到这个三角形在抛物线上新的“卡点对”.请直接写出△BOC在已知抛物线上所有“卡点对”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c过等腰Rt△OAB的A,B两点,点B在点A的右侧,直角顶点A(0,3).
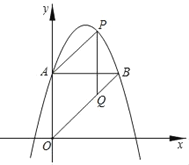
(1)求b,c的值.
(2)P是AB上方抛物线上的一点,作PQ⊥AB交OB于点Q,连接AP,是否存在点P,使四边形APQO是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com