
| A. | 16.5×103 | B. | 1.65×104 | C. | 1.65×103 | D. | 0.165×104 |
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
 如图,是长清园博园内的一个矩形花园,花园长为80米,宽为30米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为1400米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?
如图,是长清园博园内的一个矩形花园,花园长为80米,宽为30米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为1400米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:b是最小的正整数,且a,b满足(c-5)2+|a+b|=0,请回答问题:
已知:b是最小的正整数,且a,b满足(c-5)2+|a+b|=0,请回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
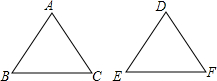 如图,下列各组条件中,不能判定△ABC≌△DEF的是( )
如图,下列各组条件中,不能判定△ABC≌△DEF的是( )| A. | AB=DE,∠A=∠D,AC=DF | B. | ∠B=∠E,AB=DE,AC=DE | ||
| C. | ∠A=∠D,AB=DE,∠B=∠E | D. | AB=DE,BC=EF,AC=DF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com