
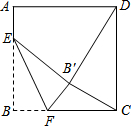
 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.分析 (1)如图1中,当∠BEF=45°时,易知四边形BEB′F是正方形,推出BF=BE,由AB=BC,即可证明CF=AE=3.
(2)如图2中,作B′N⊥BC于N,NB′的延长线交AD于M,作EG⊥MN于G,则四边形MNCD、四边形AEGM都是矩形.由△B′MD≌△B′CN,推出B′M=B′N=8,由AE=MG=3,推出GB′=5,在Rt△EGB′中,EG=$\sqrt{EB{′}^{2}-GB{′}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,由△EGB′∽△B′NF,推出$\frac{EG}{B′N}$=$\frac{EB′}{FB′}$,由此即可解决问题.
(3)如图3中,以E为圆心EB为半径画圆,在Rt△EBC中,∠EBC=90°,EB=13,BC=16,推出EC=$\sqrt{1{6}^{2}+1{3}^{2}}$=5$\sqrt{17}$,由△CFB′的周长=CF+FB′+CB′=BF+CF+CB′=BC+CB′=16+CB′,所以欲求△CFB′的周长的最小值,只要求出CB′的最小值即可,因为CB′+EB′≥EC,所以E、B′、C共线时,CB′的值最小.
解答 (1)证明:如图1中,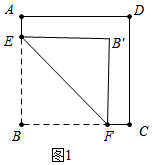
当∠BEF=45°时,易知四边形BEB′F是正方形,
∴BF=BE,
∵AB=BC,
∴CF=AE=3.
(2)解:如图2中,作B′N⊥BC于N,NB′的延长线交AD于M,作EG⊥MN于G,则四边形MNCD、四边形AEGM都是矩形.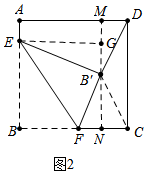
∵B′D=B′C,
∴∠B′DC=∠B′CD,
∵∠ADC=∠BCD=90°,
∴∠B′DM=∠B′CN,
∵∠B′MD=∠B′NC=90°,
∴△B′MD≌△B′CN,
∴B′M=B′N=8,
∵AE=MG=3,
∴GB′=5,
在Rt△EGB′中,EG=$\sqrt{EB{′}^{2}-GB{′}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
∵∠EB′G+∠FB′N=90°,∠FB′N+∠B′FN=90°,
∴∠EB′G=∠B′FN,∵∠EGB′=∠FNB′=90°,
∴△EGB′∽△B′NF,
∴$\frac{EG}{B′N}$=$\frac{EB′}{FB′}$,
∴$\frac{12}{8}$=$\frac{13}{B′F}$,
∴BF=B′F=$\frac{26}{3}$.
(3)解:如图3中,
以E为圆心EB为半径画圆,在Rt△EBC中,∠EBC=90°,EB=13,BC=16,
∴EC=$\sqrt{1{6}^{2}+1{3}^{2}}$=5$\sqrt{17}$,
∵△CFB′的周长=CF+FB′+CB′=BF+CF+CB′=BC+CB′=16+CB′,
∴欲求△CFB′的周长的最小值,只要求出CB′的最小值即可,
∵CB′+EB′≥EC,
∴E、B′、C共线时,CB′的值最小,CB′最小值为5$\sqrt{17}$-13.
∴△CFB′的周长的最小值为3+5$\sqrt{17}$.
点评 本题考查四边形综合题、正方形的性质与判定、全等三角形的判定和性质、三角形的三边关系定理、勾股定理、相似三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形或相似三角形解决问题,学会利用三边关系定理解决最值问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 如图,?ABCD的对角线AC、BD相交于点O,AE=CF.
如图,?ABCD的对角线AC、BD相交于点O,AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
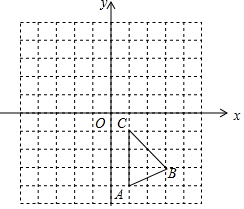 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
| 频数 | 16 | 25 | 9 | 7 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com