
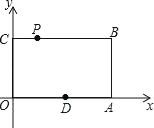
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是_____.
【答案】(3,4)或(![]() ,4)或(6﹣
,4)或(6﹣![]() ,4)
,4)
【解析】
由矩形的性质得出BC=OA=6,AB=OC=4,∠B=∠OCB=90°,分三种情况:①当PO=PA时;②当AP=AO=6时;③当OP=OA=6时;分别求出PC的长,即可得出结果.
∵四边形OABC是矩形,

∴BC=OA=6,AB=OC=4,∠B=∠OCB=90°,
分三种情况:如图所示:
①当PO=PA时,P在OA的垂直平分线上,P是BC的中点,PC=3,
∴点P的坐标为(3,4);
②当AP=AO=6时,BP=![]() ,
,
∴PC=6-2![]() ,
,
∴P(6-2![]() ,4);
,4);
③当OP=OA=6时,PC=![]() ,
,
∴P(2![]() ,4).
,4).
综上所述:点P的坐标为(3,4)或(2![]() ,4)或(6-2
,4)或(6-2![]() ,4).
,4).
故答案为:(3,4)或(2![]() ,4)或(6-2
,4)或(6-2![]() ,4).
,4).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)以原点O为位似中心,相似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1,并直接写出C1点的坐标;
(2)若点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】司机小李某天下午营运全是在东西走向的大道上行驶,如果规定向东行驶为正,向西行驶为负,这天下午行车里程如下:(单位:千米)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)被送到目的地时,小李在出发地的什么位置?
(2若每千米的营运额为8元,则这天下午的营运额为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国庆节大酬宾”,某商场设计的促销活动如下:在一个不透明的箱子里放有3个质地相同的小球,并在球上分别标有“5元”、“10元”和“15元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两个小球所标金额和返还相等价格的购物券,购物券可以在本商场消费,某顾客刚好消费300元.
(1)该顾客最多可得到元购物券;
(2)请你用画树状图和列表的方法,求出该顾客所得购物券的金额不低于25元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)数轴上点A、B表示的数分别是a、b,若a>b,则AB=a﹣b.
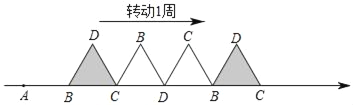
例如,若数轴上点A、B表示的两个数分别为﹣2000和+18,
则AB=18﹣(﹣2000)=18+2000=2018
(应用)若数轴上点A、B表示的两个数分别为x和﹣1,且x>﹣1,则AB= (用含x的代数式表示);
(拓展)如图,数轴上点A表示的数为﹣2a,点B表示的数为﹣![]() a,点C表示的数为﹣2,且AB=BC.
a,点C表示的数为﹣2,且AB=BC.
(1)求a的值;
(2)以BC为边作等边三角形BCD,并将共向右滚动1周得到新的等边三角形BCD,依次继续滚动…….若滚动第n周后,等边三角形BCD的顶点C表示的数是2014,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
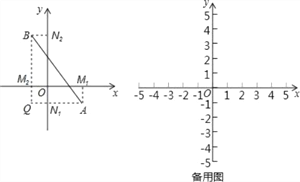
【题目】阅读材料,在平面直角坐标系中,已知x轴上两点A(x1,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:
(1)AB= .
(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为 ;
(3)根据阅读材料并利用平面内两点间的距离公式,求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com