
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.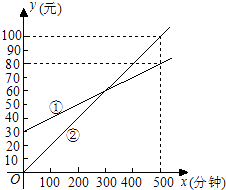
(1)有月租费的收费方式是(填①或②),月租费是元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
【答案】
(1)①;30
(2)解:设y1=k1x+30,y2=k2x,由题意得:将(500,80),(500,100)分别代入即可:
500k1+30=80,
∴k1=0.1,
500k2=100,
∴k2=0.2
故所求的解析式为y1=0.1x+30; y2=0.2x
(3)解:当通讯时间相同时y1=y2 , 得0.2x=0.1x+30,解得x=300;
当x=300时,y=60.
故由图可知当通话时间在300分钟内,选择通话方式②实惠;
当通话时间超过300分钟时,选择通话方式①实惠;
当通话时间在300分钟时,选择通话方式①、②一样实惠
【解析】(1)观察函数图像可知①的图像与y轴交点坐标为(0,30)即可得出答案。
(2)观察图像可知①的图像经过(0,30),(500,80),②的图像经过(500,100)(0,0)利用待定系数法分别建立方程组,求解即可得出①、②两种收费方式中y与自变量x之间的函数关系式。
(3)分三种情况讨论,先求出两种收费方式相同时自变量的值,再以此为界说明消费方式即可。


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的是( )
A.三点确定一个圆
B.平分弦的直径垂直于弦
C.圆有无数条对称轴,任何一条直径都是它的对称轴
D.同弧或等弧所对圆心角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B.C.D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H.
①△BCE≌△ACD;
②CF=CH;
③△CFH为等边三角形;
④FH∥BD;
⑤AD与BE的夹角为60°,
以上结论正确的是 . 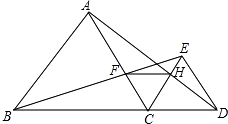
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O. 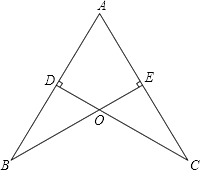
(1)求证:AD=AE;
(2)试猜想:OA与BC的位置关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A(2,0),点B (0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折![]() ,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为___________________________.
,使点C落在点D处,若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为___________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com