
���� ��1��ȡA��-1��0����B��1��0����C��0��1�����㣬�����A��B��C������������ɣ�
��2����ͼ1�У�����P��PH��AB��H����PAB�ǵȱ������Σ�����PH=$\sqrt{3}$AH���г����̼��ɽ�����⣮
��3����ͼ2�У�����ACD���APB���ڵ�A���ĶԳƣ����ı���PBCDΪƽ���ı��Σ���PC=BDʱ��ƽ���ı���PBCDΪ���Σ���PA=AB���Ƴ���APBΪ�ȱ������Σ��ɴ����D��C���꼴�ɽ�����⣮
��� �⣺��1���𰸲�Ψһ����A��-1��0����B��1��0����C��0��1��ʱ����ABC�ǵ���ֱ�������Σ���ʱ����A��B��C�����������Ϊy=-x2+1��
�ʴ�Ϊy=-x2+1��
��2����������y=-x2+bx��b��0���ġ������������Ρ��ǵȱ�ֱ�������Σ�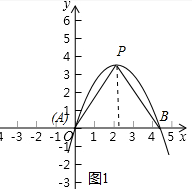
�֡߸������ߵĶ��㣨$\frac{b}{2}$��$\frac{{b}^{2}}{4}$����
��ͼ1�У�����P��PH��AB��H��
�ߡ�PAB�ǵȱ������Σ�
��PH=$\sqrt{3}$AH��
��$\frac{{b}^{2}}{4}$=$\frac{\sqrt{3}b}{2}$��
��b=2$\sqrt{3}$��
��3����ͼ2�У�����ACD���APB���ڵ�A���ĶԳƣ����ı���PBCDΪƽ���ı��Σ�
��PC=BDʱ��ƽ���ı���PBCDΪ���Σ�
��PA=AB��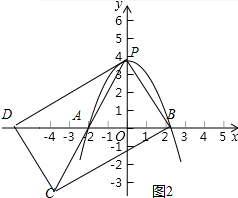
���APBΪ�ȱ������Σ�
�ɣ�2��������֪��P��0��3����
��A��-$\sqrt{3}$��0����B��$\sqrt{3}$��0����
�����ĶԳ�ͼ�ε����ʿ�֪��D��-3$\sqrt{3}$��0����C��-2$\sqrt{3}$��-3����
���O��C��D�����������Ϊy=ax2+bx��
��$\left\{\begin{array}{l}{27a-3\sqrt{3}b=0}\\{12a-2\sqrt{3}b=-3}\end{array}\right.$���$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=\frac{3\sqrt{3}}{2}}\end{array}\right.$��
��O��C��D����������ߵı���ʽΪ��y=$\frac{1}{2}$x2+$\frac{3\sqrt{3}}{2}$x��
���� ���⿼����κ����ۺ��⡢�ȱ������ε��ж������ʡ����ε��ж������ʡ�����ϵ����ȷ����������ʽ��֪ʶ������Ĺؼ��dz�����õȱ����������ʣ�����ؼ�������꣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
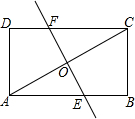 ��ͼ������ABCD�У��Խ���AC���е�ΪO����O��EF��AC���ֱ�AB��DC��E��F����AB=4��BC=2����ô�߶�EF�ij�Ϊ$\sqrt{5}$��
��ͼ������ABCD�У��Խ���AC���е�ΪO����O��EF��AC���ֱ�AB��DC��E��F����AB=4��BC=2����ô�߶�EF�ij�Ϊ$\sqrt{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
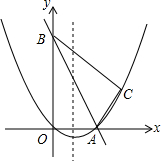 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+10��x�ᣬy���ཻ��A��B���㣬��C�������ǣ�8��4��������AC��BC��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-2x+10��x�ᣬy���ཻ��A��B���㣬��C�������ǣ�8��4��������AC��BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
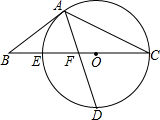 ��ͼ���ԡ�ABC��BC����һ��OΪԲ�ģ�����A��C��������BC�߽��ڵ�E����DΪCE���°�Բ�����е㣬����AD���߶�EO�ڵ�F����AB=BF��
��ͼ���ԡ�ABC��BC����һ��OΪԲ�ģ�����A��C��������BC�߽��ڵ�E����DΪCE���°�Բ�����е㣬����AD���߶�EO�ڵ�F����AB=BF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���������̽������ʾ����������A����һ��¥����B��������Ϊ30�㣬���ⶰ¥�ײ�C���ĸ���Ϊ60�㣬������A����¥��ˮƽ����Ϊ120m�����ⶰ¥�ĸ߶�Ϊ��������
��ͼ���������̽������ʾ����������A����һ��¥����B��������Ϊ30�㣬���ⶰ¥�ײ�C���ĸ���Ϊ60�㣬������A����¥��ˮƽ����Ϊ120m�����ⶰ¥�ĸ߶�Ϊ��������| A�� | 160$\sqrt{3}$m | B�� | 120$\sqrt{3}$m | C�� | 300m | D�� | 160$\sqrt{2}$m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -4 | B�� | 0.101001 | C�� | $\frac{1}{3}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com