
| A. | $\frac{m}{2}$ | B. | $\frac{n}{2}$ | C. | $\frac{m}{2}$或$\frac{{n}^{2}}{2m}$ | D. | $\frac{n}{2}$或$\frac{{m}^{2}}{2n}$ |
分析 分△APQ∽△ABC和△APQ∽△ACB两种情况,根据相似三角形的性质计算即可.
解答 解:∵P是AB的中点,
∴AP=$\frac{1}{2}$AB=$\frac{1}{2}$m,
(1)当△APQ∽△ABC时,$\frac{AP}{AB}$=$\frac{AQ}{AC}$,即$\frac{\frac{m}{2}}{m}$=$\frac{AQ}{n}$,
解得,AQ=$\frac{n}{2}$;
(2)当△APQ∽△ACB时,$\frac{AP}{AC}$=$\frac{AQ}{AB}$,即$\frac{\frac{m}{2}}{n}$=$\frac{AQ}{m}$,
解得,AQ=$\frac{{m}^{2}}{2n}$;
故选:D.
点评 本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
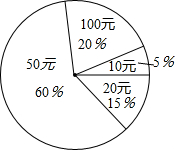 在雅安地震救灾捐款活动中,某校6000名同学每人都捐了款,有捐10元的,有捐20元的,还有捐50元、100元的,如图统计图反映了不同捐款的人数和比例,那么该校同学平均每人捐款53.5元.
在雅安地震救灾捐款活动中,某校6000名同学每人都捐了款,有捐10元的,有捐20元的,还有捐50元、100元的,如图统计图反映了不同捐款的人数和比例,那么该校同学平均每人捐款53.5元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com