
已知:如图1,矩形ABCD中,AB=6,BC=8,E、F、G、H分别是AB、BC、CD、DA四条边上的点(且不与各边顶点重合),设m=EF+FG+GH+HE,探索m的取值范围.
(1)如图2,当E、F、G、H分别是AB、BC、CD、DA四边中点时,m= .
(2)为了解决这个问题,小贝同学采用轴对称的方法,如图3,将整个图形以CD为对称轴
翻折,接着再连续翻折两次,从而找到解决问题的途径,求得m的取值范围.①请在图3
中补全小贝同学翻折后的图形;②请你根据①中的图形,求出m的取值范围,并简要说明理
由.
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
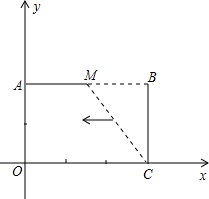 已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.
已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com