练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，梯形ABCD中， DC∥AB，点E是BC的中点，连结AE并延长与DC的延长线相交于点F，连结BF，AC.
    求证：四边形ABFC是平行四边形；
    证明略
    利用全等三角形根据平行四边形的判定来证明
    证明法一：∵DC∥AB
    ∴∠ECF=∠EBA
    ∵E是BC中点
    ∴CE=BE
    又∵∠CEF=∠BEA
    ∴△CEF≌△BEA（ASA）
    ∴CF=AB
    ∵CF∥AB
    ∴四边形ABFC是平行四边形
    证明法二：同上可得，△CEF≌△BEA（ASA）
    ∴EF=AE
    又∵CE=BE
    ∴四边形ABFC是平行四边形
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

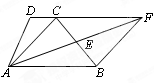
    科目：初中数学 来源：不详 题型：解答题

    如图1所示，已知在△ABD和△AEC中，，，
    小题1:如图1，试说明：≌;
    小题2:如图1，若，，，
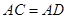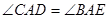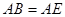
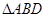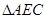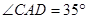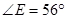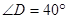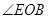    ①试求:的度数
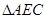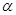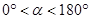    ②将绕点A逆时针旋转度（），问当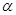为多少度时，直线CE分别与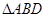的三边所在的直线垂直？（请直接写出答案）。
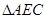    小题3:如图2将绕点A逆时针旋转后得到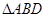，并使点D，E，A三点在同一条直线上，若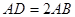，连接CD，若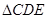的面积为6cm2，你能求出四边形ABDC的面积吗？若能，请求出来；若不能，请你说明理由。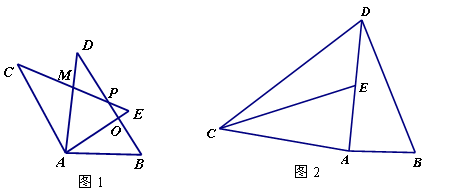

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：单选题

    如图, 梯形ABCD中，AD∥BC，对角线的交点为O，CE∥AB交BD的延长线于E，若OB=6，OD=4，则DE=（   ）
    A．12B．9C．8D．5

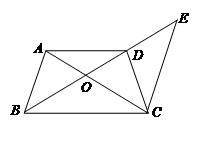
    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （本题满分10分）如图1，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿BC方向平移得到的，连接AE.AC和BE相交于点O.

    （1）判断四边形ABCE是怎样的四边形，说明理由；
    （2）如图2，P是线段BC上一动点（图2），（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R.
    ①四边形PQED的面积是否随点P的运动而发生变化？
    若变化，请说明理由；若不变，求出四边形PQED的面积；
    ②当线段BP的长为何值时，△PQR与△BOC相似？

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    已知一个多边形的内角和与它的外角和正好相等，则这个多边形是       边形.

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    ．把一个矩形剪去一个正方形，若余下的矩形与原矩形相似，则原矩形长宽之比为_____．

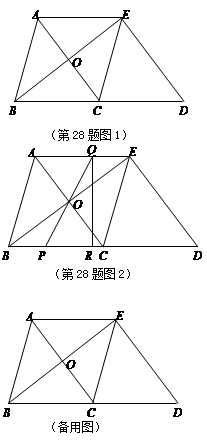
    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

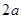    在△ABC中，BC＝a，BC边上的高h＝，沿图中线段DE、CF将△ABC剪开，分成的三块图形恰能拼成正方形CFHG，如图1所示．请你解决如下问题：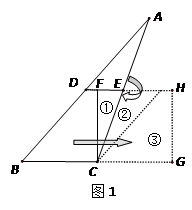

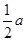    已知：如图2，在△A′B′C′中，B′C′＝a，B′C′边上的高h＝．请你设计两种不同的分割方法，将△A′B′C′沿分割线剪开后，所得的三块图形恰能拼成一个正方形，请在图2、图3中，画出分割线及拼接后的图形．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，已知四边形为平行四边形，、为对角线上的两点，且，连接。求证：。

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，将矩形纸片ABCD沿EF折叠，使A点与C点重合，点D落在点G处，EF为折痕．

    小题1:(1)求证：△FGC≌△EBC；
    小题2:(2)若AB＝8，AD＝4，求四边形ECGF(阴影部分)的面积．（7分

    查看答案和解析>>

    同步练习册答案