
【题目】已知![]() 的三边长为
的三边长为![]() ,
,![]() ,
,![]() ,有以下三个结论:(1)以
,有以下三个结论:(1)以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;(2)以
为边长的三角形一定存在;(2)以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在;(3)以
为边长的三角形一定存在;(3)以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在.其中正确结论的个数是( ).
为边长的三角形一定存在.其中正确结论的个数是( ).
A.0个B.1个C.2个D.3个
【答案】C
【解析】
不妨设0<a≤b≤c,利用作差法求出(![]() +
+![]() )2-(
)2-(![]() )2的符号和三角形的三边关系即可判断(1);利用举反例的方法即可判断(2);假设
)2的符号和三角形的三边关系即可判断(1);利用举反例的方法即可判断(2);假设![]() ≤
≤![]() ≤
≤![]() ,根据绝对值的性质:
,根据绝对值的性质:![]() 和三角形的三边关系,即可得出结论.
和三角形的三边关系,即可得出结论.
解:![]() 的三边长为
的三边长为![]() ,
,![]() ,
,![]() ,不妨设0<a≤b≤c,
,不妨设0<a≤b≤c,
∴a+b>c,![]() <
<![]() <
<![]()
则(![]() +
+![]() )2-(
)2-(![]() )2
)2
=![]()
=![]()
∵![]()
∴![]() >0
>0
∴(![]() +
+![]() )2>(
)2>(![]() )2
)2
∴![]() +
+![]() >
>![]()
∴以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在,故(1)正确;
为边长的三角形一定存在,故(1)正确;
令a=2,b=3,c=4,此时a+b>c,符合条件
此时![]() +
+![]() =13,
=13,![]() =16,
=16,
∴![]() +
+![]() <
<![]()
∴以![]() ,
,![]() ,
,![]() 为边长的三角形不一定存在,故(2)错误;
为边长的三角形不一定存在,故(2)错误;
假设![]() ≤
≤![]() ≤
≤![]()
根据绝对值的性质:![]() +
+![]() ≥
≥![]() =
=![]()
∴![]() +
+![]() +2>
+2>![]()
∴![]() +
+![]() >
>![]()
∴以![]() ,
,![]() ,
,![]() 为边长的三角形一定存在,故(3)正确.
为边长的三角形一定存在,故(3)正确.
综上:正确的有2个
故选C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出
四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出![]() 厂家的合格率为
厂家的合格率为![]() ,并根据检测数据绘制了两幅不完整的统计图.
,并根据检测数据绘制了两幅不完整的统计图.
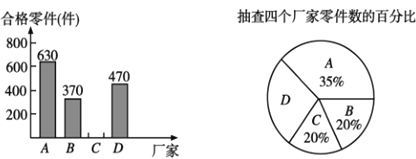
(1)抽查![]() 厂家的零件为______件,扇形统计图中
厂家的零件为______件,扇形统计图中![]() 厂家对应的圆心角为______.
厂家对应的圆心角为______.
(2)抽查![]() 厂家的合格零件为_______件.
厂家的合格零件为_______件.
(3)若要从![]() ,
,![]() ,
,![]() ,
,![]() 四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出
四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用列表法或画树状图的方法求出![]() ,
,![]() 两个厂家同时被选中的概率,并列出所有等可能的结果.
两个厂家同时被选中的概率,并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能是来自太阳的辐射能量,对于地球上的人类来说,太阳能是对环境无任何污染的可再生能源,因此许多国家都在大陆发展太阳能.如图是2013-2017年我国光伏发电装机容量统计图.根据统计图提供的信息,判断下列说法不合理的是( )
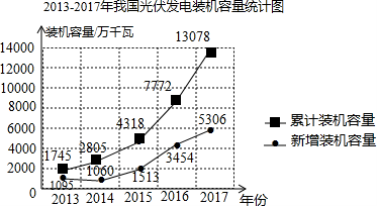
A.截至2017年底,我国光伏发电累计装机容量为13078万千瓦
B.2013-2017年,我国光伏发电新增装机容量逐年增加
C.2013-2017年,我国光伏发电新增装机容量的平均值约为2500万千瓦
D.2017年我国光伏发电新增装机容量大约占当年累计装机容量的40%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是线段OB、OC上的动点
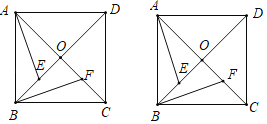
(1)如果动点E、F满足BE=OF(如图),且AE⊥BF时,问点E在什么位置?并证明你的结论;
(2)如果动点E、F满足BE=CF(如图),写出所有以点E或F为顶点的全等三角形(不得添加辅助线).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化“携手节能低碳,共建碧水蓝天”活动,发展“低碳经济”,某单位进行技术革新,让可再生资源重新利用.今年1月份,再生资源处理量为40吨,从今年1月1日起,该单位每月再生资源处理量每一个月将提高10吨.月处理成本![]() (元)与月份
(元)与月份![]() (月)之间的关系可近似地表示为:
(月)之间的关系可近似地表示为:![]() ,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为
,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为![]() (吨),每月的利润为
(吨),每月的利润为![]() (元).
(元).
(1)分别求出![]() 与
与![]() ,
,![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)在今年内该单位哪个月获得利润达到5800元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红参加学校组织的庆祝党的十九大胜利召开知识竞赛,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,可是小红这两道题都不会,不过竞赛规则规定每位选手有两次求助机会,使用“求助”一次可以让主持人去掉其中一题的一个错误选项,主持人提醒小红可以使用两次“求助”.
(1)如果小红两次“求助”都在第一道题中使用,那么小红通关的概率是 .
(2)如果小红将每道题各用一次“求助”,请用树状图或者列表来分析她顺序通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=4,以BC为直径的半圆O交斜边AB于点 D.
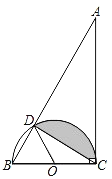
(1)证明:AD=3BD;
(2)求弧BD的长度;
(3)求阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com