练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，平行四边形ABCD中，E是边BC的中点，AE交BD于点F，如果BF=4，那么FD=8．

    分析 由平行四边形ABCD得AD=BC，AD∥BC，于是得到△ADF∽△EBF，根据相似三角形的性质便得到结论．

    解答 解：∵平行四边形ABCD，E是边BC的中点，
    ∴AD=BC，
    ∴AD∥BC，
    ∴$\frac{BE}{AD}=\frac{1}{2}$，
    ∴△ADF∽△EBF，
    ∴$\frac{BF}{DF}=\frac{BE}{AD}=\frac{1}{2}$，
    ∵BF=4，
    ∴DF=8，
    故答案为8．

    点评 本题主要考查了平行四边形和相似三角形的判定和性质，灵活应用这些性质是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    16．按如图所示的操作步骤，若输出的值为4，则输入的x值为0或-6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．已知函数y=ax2+bx+c的图象如图所示：则△＞0；a＞0；b＜0；c＜0；a+b+c＜0；a-b+c＞0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．抛物线y=-5x2+x+7与坐标轴的交点个数是（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，在Rt△ABC中，∠C=90°，正方形DEFG的顶点D，E在AB边上，F，G分别在BC和AC上，若AD=4，BE=1，求：
    （1）DE的长．
    （2）AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．在?ABCD中，AE交BC的延长线于点E，交DC于点F，若BC：CE=3：2，则CF：FD=$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

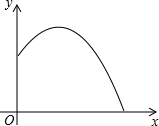    18．如图是某运动员打羽毛球的抛物线示意图，已知打出羽毛球的高度y（m）与水平距离x（m）之间的函数关系式是y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+7，则该羽毛球落地时距离发出点（　　）
    A．6mB．7mC．8mD．9m

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

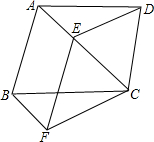    11．如图，四边形ABCD的AB边平行于CD边，在对角线上取一点E，使∠DEC=∠ABC，若CE：CD=CD：CA．
    （1）问：AD和BC有什么关系？
    （2）先作EF∥AB，再作BF∥AC，使得BF交FE于点F，连接CF，有∠DCE=∠BCF．试判断CDEF的形状，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

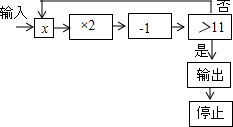    12．如图为某一运算程序，规定：程序运行到判断“结果是否大于11”为一次运算，若输入整数x后，运算进行了2次就输出停止，则满足条件的整数x是4、5或6．

    查看答案和解析>>

    同步练习册答案