
【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证: ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

【答案】(1)证明见解析;(2)![]() c(a+b﹣c);(3)证明见解析.
c(a+b﹣c);(3)证明见解析.
【解析】试题分析:(1)首先过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,可得△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,则可求得BN=![]() b,DM=
b,DM=![]() a,继而求得答案;
a,继而求得答案;
(2)由S△AMN=S△ABD-S△ABM-S△ADN,可得S△AMN=![]() c2-
c2-![]() c(c-a)-
c(c-a)-![]() c(c-b),继而求得答案;
c(c-b),继而求得答案;
(3)易证得∴∠DMA=∠BAN,又由∠ABD=∠ADB=45°,可证得△ADM∽△NBA,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)证明:过点N作NH⊥AB于点H,过点M作MI⊥AD于点I,
∵四边形ABCD是正方形,
∴∠ADB=∠ABD=45°,
∴△NHB和△DIM是等腰直角三角形,四边形AGNH和四边形AEMI是矩形,
∴BN=![]() NH=
NH=![]() AG=
AG=![]() b,DM=
b,DM=![]() MI=
MI=![]() AE=
AE=![]() a,
a,
∴![]() ;
;
(2)S△AMN=S△ABD﹣S△ABM﹣S△ADN
=![]() ABAD﹣
ABAD﹣![]() ABME﹣
ABME﹣![]() ADNG
ADNG
=![]() c2﹣
c2﹣![]() c(c﹣a)﹣
c(c﹣a)﹣![]() c(c﹣b)
c(c﹣b)
=![]() c(c﹣c+a﹣c+b)
c(c﹣c+a﹣c+b)
=![]() c(a+b﹣c);
c(a+b﹣c);
(3)∵∠DMA=∠ABD+∠MAB=∠MAB+45°,∠BAN=∠MAB+∠MAN=∠MAB+45°,
∴∠DMA=∠BAN,
∵∠ABD=∠ADB=45°,
∴△ADM∽△NBA,
∴![]() ,
,
∵DM=![]() a,BN=
a,BN=![]() b,
b,
∴c2=2ab.



科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
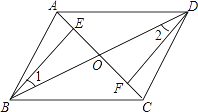
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H.
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.
①四边形BEHC是怎样的特殊四边形?证明你的结论.
②当AB与BC的比值为 时,四边形BEHC为菱形.
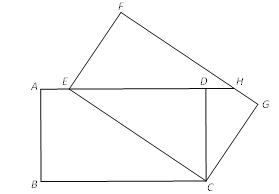
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图1,若![]() ,则
,则![]() .
.
理由:如图,过点![]() 作
作![]() ,
,
则![]() .
.
因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.

交流:(1)若将点![]() 移至图2所示的位置,
移至图2所示的位置,![]() ,此时
,此时![]() 、
、![]() 、
、![]() 之间有什么关系?请说明理由.
之间有什么关系?请说明理由.
探究:(2)在图3中,![]() ,
,![]() 、
、![]() 又有何关系?
又有何关系?
应用:(3)在图4中,若![]() ,又得到什么结论?请直接写出该结论.
,又得到什么结论?请直接写出该结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E为正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,那么∠AFC的度数为( )
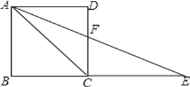
A. 112.5° B. 125° C. 135° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三个点![]() ,
,![]() 是
是![]() 的边
的边![]() 上一点,
上一点,![]() 经平移后得到
经平移后得到![]() ,点
,点![]() 的对应点为
的对应点为![]() .
.
(1)画出平移后的![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(2)![]() 的面积为_________________;
的面积为_________________;
(3)若点![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的关系式(用含
之间的关系式(用含![]() 的式子表示
的式子表示![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设x1、x2是一元二次方程2x2﹣7x+5=0的两根,利用一元二次方程根与系数的关系,求下列各式的值.
(1)x12x2+x1x22; (2)(x1﹣x2)2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com