
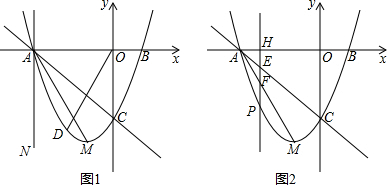
分析 (1)根据顶点坐标列出关于b、c的方程组求解可得,由抛物线解析式求得A、C坐标,利用待定系数法可得直线AC解析式;
(2)①设点D的坐标为(m,m2+2m-3),由∠COD=∠MAN得tan∠COD=tan∠MAN,列出关于m的方程求解可得;②求出直线AM的解析式,进而可用含t的式子表示出HE、EF、FP的长度,根据等腰三角形定义即可判定;由等腰三角形底角的余弦值为$\frac{3}{5}$可得$\frac{\frac{1}{2}FP}{EF}$=$\frac{3}{5}$,列方程可求得t的值.
解答 解:(1)∵抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),
∴$\left\{\begin{array}{l}{-\frac{b}{2}=-1}\\{\frac{4c-{b}^{2}}{4}=-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=2}\\{c=-3}\end{array}\right.$,
∴抛物线解析式为:y=x2+2x-3,
令y=0,得:x2+2x-3=0,解得:x1=1,x2=-3,
∴A(-3,0),B(1,0),
令x=0,得y=-3,
∴C(0,-3),
设直线AC的解析式为:y=kx+b,
将A(-3,0),C(0,-3)代入,
得:$\left\{\begin{array}{l}{-3k+b=0}\\{b=-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=-3}\end{array}\right.$,
∴直线AC的解析式为:y=-x-3;
故答案为:2,-3,y=-x-3.
(2)①设点D的坐标为(m,m2+2m-3),
∵∠COD=∠MAN,
∴tan∠COD=tan∠MAN,
∴$\frac{-m}{-({m}^{2}+2m-3)}$=$\frac{2}{4}$,
解得:m=±$\sqrt{3}$,
∵-3<m<0,
∴m=-$\sqrt{3}$,
故点D的坐标为(-$\sqrt{3}$,-2$\sqrt{3}$);
②设直线AM的解析式为y=mx+n,
将点A(-3,0)、M(-1,-4)代入,
得:$\left\{\begin{array}{l}{-3m+n=0}\\{-m+n=-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=-2}\\{n=-6}\end{array}\right.$,
∴直线AM的解析式为:y=-2x-6,
∵当x=t时,HE=-(-t-3)=t+3,HF=-(-2t-6)=2t+6,HP=-(t2+2t-3),
∴HE=EF=HF-HE=t+3,FP=-t2-4t-3,
∵HE+EF-FP=2(t+3)+t2+4t+3=(t+3)2>0,
∴HE+EF>FP,
又HE+FP>EF,EF+FP>HE,
∴当-3<t<-1时,线段HE,EF,FP总能组成等腰三角形;
由题意得:$\frac{\frac{1}{2}FP}{EF}$=$\frac{3}{5}$,即$\frac{\frac{1}{2}(-{t}^{2}-4t-3)}{t+3}$=$\frac{3}{5}$,
整理得:5t2+26t+33=0,
解得:t1=-3,t2=-$\frac{11}{5}$,
∵-3<t<-1,
∴t=-$\frac{11}{5}$.
点评 本题主要考查了待定系数法求二次函数解析式函数图象交点的求法等知识点、等腰三角形的判定等知识点,主要考查学生数形结合的数学思想方法.综合性强.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )
如图,某小区规划在一个长AD=40m,宽AB=26m的矩形场地ABCD上修建三条同样宽的通道(图中阴影部分),使其中两条与AB平行,另一条与AD平行,其余部分种植花草,要使每一块种植花草的场地面积都是144m2.若设通道的宽度为x(m),则根据题意所列的方程是( )| A. | (40-x)(26-2x)=144×6 | B. | (40-2x)(26-x)=144×6 | C. | (40-2x)(26-x)=144÷6 | D. | (40-x)(26-2x)=144÷6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,三张卡片形状、大小、质地相同,分别印数字1、2、3,现将它们放入盒子.若从盒子中任取一张卡片,求取到数字是奇数的卡片的概率是$\frac{2}{3}$.
如图,三张卡片形状、大小、质地相同,分别印数字1、2、3,现将它们放入盒子.若从盒子中任取一张卡片,求取到数字是奇数的卡片的概率是$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg-5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg-5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )
已知M、N、P、Q四点的位置如图所示,下列结论中,正确的是( )| A. | ∠NOQ=42° | B. | ∠NOP=132° | C. | ∠PON比∠MOQ大 | D. | ∠MOQ与∠MOP互补 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| “读书节”活动计划书 | ||
| 书本类别 | A类 | B类 |
| 进价(单位:元) | 18 | 12 |
| 备注 | 1、用不超过16800元购进A、B两类图书共1000本; 2、A类图书不少于600本; … | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com