
分析 (1)原式利用减法法则变形,计算即可得到结果;
(2)原式先计算乘法运算,再计算加减运算即可得到结果;
(3)原式利用除法法则变形,再利用乘法分配律计算即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=3-5-4+2=-4;
(2)原式=27-40=-13;
(3)原式=(-$\frac{2}{3}$+$\frac{1}{6}$-$\frac{1}{2}$)×18=-12+3-9=-18;
(4)原式=-4+(1-$\frac{1}{25}$)×(-$\frac{1}{8}$)=-4-$\frac{3}{25}$=-$\frac{103}{25}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
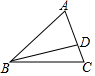 如图,已知在△ABC中,点D在边AC上,CD:AD=1:2,$\overrightarrow{BA}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$.
如图,已知在△ABC中,点D在边AC上,CD:AD=1:2,$\overrightarrow{BA}=\overrightarrow{a}$,$\overrightarrow{BC}=\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.请完整填上结论或依据.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.请完整填上结论或依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
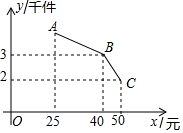 今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=-$\frac{1}{20}$x+m(m为常数).
今年是“精准扶贫”攻坚关键年,某扶贫工作队为对口扶贫村引进建立了一村集体企业,并无偿提供一笔无息贷款作为启动资金,双方约定:①企业生产出的产品全部由扶贫工作队既是联系商家收购;②企业从生产销售的利润中,要保证按时发放工人每月最低工资32000元.已知该企业生产的产品成本为20元/件,月生产量y(千件)与出厂价x(元)(25≤x≤50)的函数关系可用图中的线段AB和BC表示,其中AB的解析式为y=-$\frac{1}{20}$x+m(m为常数).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com