
【题目】如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
(1)求∠E的度数.
(2)请猜想∠A与∠E之间的数量关系,请说明理由.
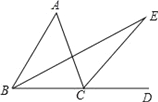
【答案】(1)∠E=20°;(2)∠A=2∠E.理由见解析.
【解析】
(1)由角平分线定义可得∠ABC=2∠CBE,∠ACD=2∠DCE,再根据三角形外角的性质可得∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,从而可得∠A=2∠E,继而可得∠E的度数;
(2)由角平分线定义可得∠ABC=2∠CBE,∠ACD=2∠DCE,再根据三角形外角的性质可得∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,从而可得∠A=2∠E.
(1)∵BE平分∠ABC,CE平分∠ACD,
∴∠ABC=2∠CBE,∠ACD=2∠DCE,
由三角形的外角性质得,∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,
∴∠A+∠ABC=2(∠E+∠CBE),
∴∠A=2∠E,
∵∠A=40°,
∴∠E=20°;
(2)∠A=2∠E,理由如下:
∵BE平分∠ABC,CE平分∠ACD,
∴∠ABC=2∠CBE,∠ACD=2∠DCE,
由三角形的外角性质得,∠ACD=∠A+∠ABC,∠DCE=∠E+∠CBE,
∴∠A+∠ABC=2(∠E+∠CBE),
∴∠A=2∠E.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
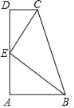
【题目】如图,AB∥CD,∠A=90°,E是AD边中点,CE平分∠BCD.
(1)求证:BE平分∠ABC;
(2)若AB=2,CD=1,求BC长;
(3)若△BCE的面积为6,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小亮从家步行到公交车站台,乘公交车去学校. 图中的折线表示小亮的离家距离s(km)与所花时间t(min)之间的函数关系. 下列说法错误的是

A. 他离家8km共用了30min B. 公交车的速度是350m/min
C. 他步行的速度是100m/min D. 他等公交车时间为6min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题: 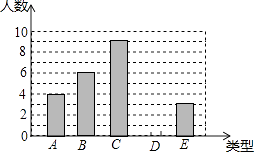
(1)补全条形统计图;
(2)求这30名职工捐书本数的平均数、众数和中位数;
(3)估计该单位750名职工共捐书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
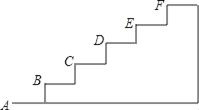
【题目】如图是某台阶的一部分,如果A点的坐标为(0,0),B点的坐标为(1,1),
(1)请建立适当的直角坐标系,并写出其余各点的坐标;
(2)如果台阶有10级,请你求出该台阶的长度和高度;
(3)若这10级台阶的宽度都是2m,单位长度为1m,现要将这些台阶铺上地毯,需要多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com