
【题目】如图,点O是直线AB上的一点,OD⊥OC,过点O作射线OE平分∠BOC.
(1)如图1,如果∠AOC=50°,依题意补全图形,写出求∠DOE度数的思路(不需要写出完整的推理过程);
(2)当OD绕点O顺时针旋转一定的角度得到图2,使得直角边OC在直线AB的上方,若∠AOC=α,其他条件不变,依题意补全图形,并求∠DOE的度数(用含α的代数式表示);
(3)当OD绕点O继续顺时针旋转一周,回到图1的位置,在旋转过程中你发现∠AOC与∠DOE(0°≤∠AOC≤180°,0°≤∠DOE≤180°)之间有怎样的数量关系?请直接写出你的发现.

【答案】(1)见解析;(2)补图见解析,∠DOE=![]() α;(3)∠DOE=
α;(3)∠DOE=![]() ∠AOC或∠DOE=180°
∠AOC或∠DOE=180°![]() ∠AOC.
∠AOC.
【解析】
(1)根据角平分线的作法作出OE平分∠BOC,先根据平角的定义求出∠BOC,再根据角平分线的定义求出∠COE,再根据直角的定义即可求解;
(2)先根据平角的定义求出∠BOC,再根据角平分线的定义求出∠COE,再根据直角的定义即可求解;
(3)分两种情况:0°≤∠AOC≤180°,0°≤∠DOE≤180°,可求∠AOC与∠DOE之间的数量关系.
(1)如图1,补全图形:
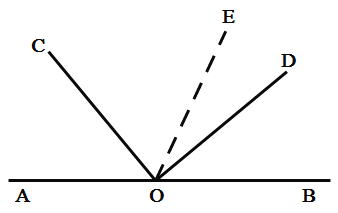
解题思路如下:
由∠AOC+∠BOC=180°,∠AOC=50°,
得∠BOC=130°;
由OE平分∠BOC,
得∠COE=65°;
由直角三角板,得∠COD=90°;
由∠COD=90°,∠COE=65°
得∠DOE=25°.
(2)如图,
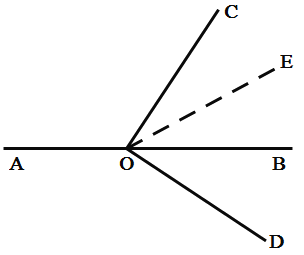
∵∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°-α;
∵OE平分∠BOC,
∴∠COE=90°-![]() α;
α;
∵OD⊥OC,
∴∠COD=90°;
∴∠DOE=∠COD-∠COE=90°-(90°-![]() α)=
α)= ![]() α;
α;
(3)由(1)、(2)可得∠DOE=![]() ∠AOC(0°≤∠AOC≤180°),∠DOE=180°
∠AOC(0°≤∠AOC≤180°),∠DOE=180°![]() ∠AOC(0°≤∠DOE≤180°).
∠AOC(0°≤∠DOE≤180°).


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图所示为一种吸水拖把,它由吸水部分、拉手部分和主干部分构成.小明在拖地中发现,拉手部分在一拉一放的过程中,吸水部分弯曲的角度会发生变化。设拉手部分移动的距离为![]() 吸水部分弯曲所成的角度为
吸水部分弯曲所成的角度为![]() ,经测量发现:拉手部分每移动
,经测量发现:拉手部分每移动![]() ,吸水部分角度变化
,吸水部分角度变化![]() .请回答下列问题:
.请回答下列问题:

(1)求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)当吸水部分弯曲所成的角度为![]() 时,求拉手部分移动的距离.
时,求拉手部分移动的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形![]() 中,点
中,点![]() 沿着边按
沿着边按![]() .方向运动,开始以每秒
.方向运动,开始以每秒![]() 个单位匀速运动、
个单位匀速运动、![]() 秒后变为每秒
秒后变为每秒![]() 个单位匀速运动,
个单位匀速运动,![]() 秒后恢复原速匀速运动,在运动过程中,
秒后恢复原速匀速运动,在运动过程中,![]() 的面积
的面积![]() 与运动时间
与运动时间![]() 的函数关系如图所示.
的函数关系如图所示.

(1)直接写出长方形的长和宽;
(2)求![]() ,
,![]() ,
,![]() 的值;
的值;
(3)当![]() 点在
点在![]() 边上时,直接写出
边上时,直接写出![]() 与
与![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,逆命题是真命题的个数有( )
①个位上的数字为0的整数能被5整除;②全等三角形的对应边相等; ③若![]() 则
则![]() ; ④面积相等的两个三角形全等;⑤全等三角形的周长相等;⑥对顶角相等,
; ④面积相等的两个三角形全等;⑤全等三角形的周长相等;⑥对顶角相等,
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
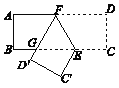
【题目】已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C,D分别落在边BC下方的点C′,D′处,且点C′,D′,B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G. 当AB=5时,△EFG的周长为_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( ).

A.126°B.110°C.108°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=10cm,BC=5cm,线段PQ=AB,点P、Q分别在AC和与AC垂直的射线AM上移动,当AP= ________ 时,△ABC和△QPA全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com