
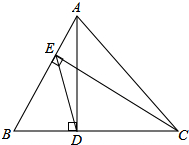
 如图.已知锐角△ABC,AD、CE分别是BC、AB边上的高,△ABC和△BDE的面积分别是27和3,DE=6$\sqrt{2}$.
如图.已知锐角△ABC,AD、CE分别是BC、AB边上的高,△ABC和△BDE的面积分别是27和3,DE=6$\sqrt{2}$.分析 (1)由已知条件得到∠CEB=∠ABD=90°,推出△ABD∽△CEB,根据相似三角形的性质得到$\frac{DB}{AB}=\frac{BE}{BC}$,可证得结论;
(2)由(1)知△ABD∽△CEB得到$\frac{{S}_{△BDE}}{{S}_{△ABC}}=(\frac{DE}{AC})^{2}$,于是求得AC,然后根据三角形的面积公式即可得到结果.
解答 (1)证明:∵AD⊥BC于D,CE⊥AB于E,
∴∠CEB=∠ABD=90°,
∵∠B=∠B,
△ABD∽△CEB,
∴△BED∽△BCA;
(2)解:由(1)知△BDE∽△BAC,
∴$\frac{{S}_{△BDE}}{{S}_{△ABC}}$=($\frac{DE}{AC}$)2,
∵△ABC和△BDE的面积分别为27和3,DE=6$\sqrt{2}$,
∴AC=18$\sqrt{2}$,
∴点B到直线AC的距离=$\frac{2{S}_{△ABC}}{AC}$=$\frac{3\sqrt{2}}{2}$.
点评 本题考查了相似三角形的判定和性质,三角形的面积的计算,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:选择题
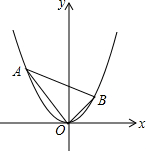 如图,点A(a,b)是抛物线y=$\frac{1}{2}$x2上位于第二象限的一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中,以下结论:①ac为定值;②ac=-bd;③△AOB的面积为定值;④直线AB必过一定点.其中正确的结论有( )
如图,点A(a,b)是抛物线y=$\frac{1}{2}$x2上位于第二象限的一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中,以下结论:①ac为定值;②ac=-bd;③△AOB的面积为定值;④直线AB必过一定点.其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ac2<bc2 | B. | c-a<c-b | C. | a-c<b-c | D. | $\frac{a}{c}<\frac{b}{c}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的格点中任取一点C,使△ABC为等腰三角形的概率是( )
如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的格点中任取一点C,使△ABC为等腰三角形的概率是( )| A. | $\frac{5}{7}$ | B. | $\frac{2}{5}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (v+1.5)km/h | B. | (v-1.5)km/h | C. | (v+3)km/h | D. | (v-3)km/h |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com