
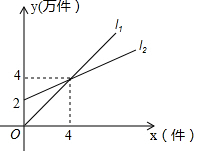
 如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本)
如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.则销售收入y1与销售量之间的函数关系式y1=x,销售成本y2与销售量之间的函数关系式y2=$\frac{1}{2}$x+2,当一天的销售量超过x>4时,生产该产品才能获利.(提示:利润=收入-成本) 分析 首先设y2=kx+2,y1=ax,再分别把(4,4)点代入可得k和a的值,进而可得函数解析式,再根据收入>成本列出不等式,可解出x的值,进而可得获利时的销售量的范围.
解答 解:设y2=kx+2,y1=ax,
∵把(4,4)代入y2=kx+2得:4=4k+2,k=$\frac{1}{2}$,
∴y2=$\frac{1}{2}$x+2;
∵把(4,4)代入y1=ax得:a=1,
∴y1=x,
∴要使销售收入超过成本,工厂能获利,必须y1>y2,
即x>$\frac{1}{2}$x+2,
x>4,
故答案为:y1=x;y2=$\frac{1}{2}$x+2;x>4.
点评 本题考查利用函数的图象解决实际问题,理解两函数图象的交点的意义是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
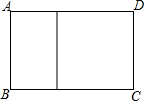 如图,用长120cm的木条制成如图形状的矩形框(矩形框中间有一横档).设矩形框的宽AB为x(cm),所围成的面积为S(cm2).
如图,用长120cm的木条制成如图形状的矩形框(矩形框中间有一横档).设矩形框的宽AB为x(cm),所围成的面积为S(cm2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠ABC=∠ADC,BE,DF分别平分∠ABC,∠ADC,且∠1=∠2,请说明:∠A=∠C.
如图,已知∠ABC=∠ADC,BE,DF分别平分∠ABC,∠ADC,且∠1=∠2,请说明:∠A=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com