
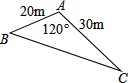
 某校的校园内有一块尺寸如图所示的三角形空地,现计划将这块空地建成一个花园.已知每平方米的造价为30元.则学校建这个花园需要投资(
某校的校园内有一块尺寸如图所示的三角形空地,现计划将这块空地建成一个花园.已知每平方米的造价为30元.则学校建这个花园需要投资(| 2 |
| 3≈1.732 |
| A、7794元 |
| B、7820元 |
| C、7822元 |
| D、7921元 |
| 3 |
| 3 |
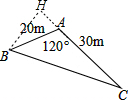 解:作BH⊥CA于H,如图,
解:作BH⊥CA于H,如图,| BH |
| AB |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
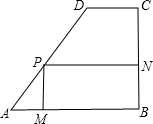 BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(48):2.7 最大面积是多少(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第6章《二次函数》中考题集(51):6.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(52):2.8 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com