
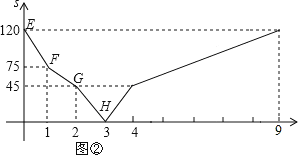
【题目】如图①,在矩形 ABCD中,AB=30cm,BC=60cm.点P从点A出发,沿A→B→C→D路线向点D匀速运动,到达点D后停止;点Q从点D出发,沿 D→C→B→A路线向点A匀速运动,到达点A后停止.若点P、Q同时出发,在运动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.

(1)请解释图中点H的实际意义?
(2)求P、Q两点的运动速度;
(3)将图②补充完整;
(4)当时间t为何值时,△PCQ为等腰三角形?请直接写出t的值.
【答案】(1)图中点H的实际意义:P、Q两点相遇;(2) P点速度为30cm/s,Q点速度为15cm/s;(3)补图见解析;(4)t=![]() 或t=5或t=8秒时,△PCQ为等腰三角形.
或t=5或t=8秒时,△PCQ为等腰三角形.
【解析】
试题分析:(1)根据P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象得出H点时两点相遇;
(2)利用函数图象得出当两点在F点到G点两点路程随时间变化减慢得出此时Q点停留,只有P点运动,再利用纵坐标的值得出P点和Q点运动速度;
(3)根据4秒后,P点到达D点,只有Q点运动,根据运动速度为15cm/s,还需要运动120-45=75(cm),则运动时间为:75÷15=5(s),进而画出图象即可;
(4)根据Q,P的位置不同,进行分类讨论得出答案即可.
试题解析:(1)图中点H的实际意义:P、Q两点相遇;
(2)由函数图象得出,当两点在F点到G点两点路程随时间变化减慢得出此时Q点停留1秒,只有P点运动,此时纵坐标的值由75下降到45,
故P点运动速度为:30cm/s,再根据E点到F点S的值由120变为75,根据P点速度,得出Q点速度为120-75-30=15(cm/s),
即P点速度为30cm/s,Q点速度为15cm/s;
(3)如图所示:根据4秒后,P点到达D点,只有Q点运动,根据运动速度为15cm/s,
还需要运动120-45=75(cm),则运动时间为:75÷15=5(s),画出图象即可;
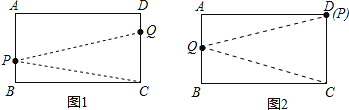
(4)如图1所示,
当QP=PC,此时![]() QC=BP,即30-30t=
QC=BP,即30-30t=![]() (30-15t),
(30-15t),
解得:t=![]() ,
,
故当时间t=![]() 时,△PCQ为等腰三角形,
时,△PCQ为等腰三角形,
如图2所示,
当D,P重合,QD=QC时,
Q为AB中点,则运动时间为:(15+60+30)÷15+1=8(s),
故当时间t=8s时,△PCQ为等腰三角形.
若PC=CQ
故90-30t=30-15t
解得:t=4
则4+1=5(S)
综上所述:t=![]() 或t=5或t=8秒时,△PCQ为等腰三角形.
或t=5或t=8秒时,△PCQ为等腰三角形.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒.
(1)用含t的代数式表示P点对应的数:___________;
用含t的代数式表示点P和点C的距离:PC=_____________
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回点A,
①点P、Q同时运动运动的过程中有__________处相遇,相遇时t=_______________秒。
②在点Q开始运动后,请用t的代数式表示P、Q两点间的距离。(友情提醒:注意考虑P、Q的位置)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.

(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填在表示它所在的集合里:
![]() ,-(-6),
,-(-6), ![]()
(1)正分数集合: { …};
(2)非负数集合: { …};
(3)整数集合: { …};
(4)非负整数集合:{ …};
(5)有理数集合: { …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了丰富学生的校园生活,准备购进一批篮球和足球.其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相等.
(1)篮球和足球的单价各是多少元?
(2)该校打算用1000元购买篮球和足球,问恰好用完1000元,并且篮球、足球都买有的购买方案有哪几种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com