
【题目】图1,是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图2的形状拼成一个正方形.



(1)图2中的阴影部分的面积为 ;
(2)观察图2,三个代数式![]() ,
,![]() ,
,![]() 之间的等量关系是 ;
之间的等量关系是 ;
(3)若![]() ,
,![]() ,求
,求![]() ;
;
(4)观察图3,你能得到怎样的代数恒等式呢?
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.

(1)∠ABE=15°, ∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为80,BD=16,求E到BC边的距离为多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格中,每个小正方形的边长都为1,网格中有两个格点![]() 、
、![]() 和直线
和直线![]() ,且
,且![]() 长为3.6.
长为3.6.
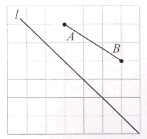
(1)求作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .
.
(2)![]() 为直线
为直线![]() 上一动点,在图中标出使
上一动点,在图中标出使![]() 的值最小的
的值最小的![]() 点,且求出
点,且求出![]() 的最小值?
的最小值?
(3)求![]() 周长的最小值?
周长的最小值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在O处开出一记手跑高球,球从地面1.4米的A处抛出(A在y轴上),运动员甲在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面3.2米高,球落地点为C点.
(1)求足球开始抛出到第一次落地时,该抛物线的解析式.
(2)足球第一次落地点C距守门员多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD内接于⊙O,AC为⊙O的直径,AC与BD交于点E,且AE=AB.
(1)DA=DB,求证:AB=CB;
(2)如图2,△ABC绕点C逆时针旋转30°得到△FGC,点A经过的路径为![]() ,若AC=4,求图中阴影部分面积S;
,若AC=4,求图中阴影部分面积S;
(3)在(2)的条件下,连接FB,求证:FB为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为半径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D
关AC对称,DF⊥DE于点D,并交EC的延长线与点F.下列结论:①CE=CF;②线段EF的最小值为2![]()
③当AD=2时,EF与半圆相切;④当点D从点A运动到点B时,线段EF扫过的面积是16![]() .其中正
.其中正
确的结论()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】踏春时节,某班学生集体组织亲子游,沿着瓯江口樱花步道骑自行车,该班学生花了950元租了若干辆自行车,已知自行车的类型和租车价格如下表:
自行车类型 |
|
|
|
座位教(个) | 2 | 3 | 4 |
租车价格(元/辆) | 30 | 45 | 55 |
(1)若同时租用![]() 、
、![]() 两种类型的车,且共有65个座位,则应租
两种类型的车,且共有65个座位,则应租![]() 、
、![]() 类型车各多少辆?
类型车各多少辆?
(2)若![]() 型车租4辆,余下的租用
型车租4辆,余下的租用![]() 型和
型和![]() 型,要求每种车至少租用1辆,请你帮他们设计
型,要求每种车至少租用1辆,请你帮他们设计![]() 型车和
型车和![]() 型车的租车方案.
型车的租车方案.
(3)若同时租用这三类车,且每种车至少租用1辆,则最多能租到______个座位.(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com