
【题目】我们把如图1所示的菱形称为基本图形,将此基本图形不断复制并平移,使得相邻两个基本图形的一个顶点与对称中心重合,得到的所有菱形都称为基本图形的特征图形,显然图2中有3个特征图形.

(1)观察以上图形并完成如表:
根据表中规律猜想,图n(n≥2)中特征图形的个数为 .(用含n的式子表示)
图形名称 | 基本图形的个数 | 特征图形的个数 |
图1 | 1 | 1 |
图2 | 2 | 3 |
图3 | 3 | 7 |
图4 | 4 | |
…… | …… | …… |
(2)若基本图形的面积为2,则图2中小特征图形的面积是 ;图2020中所有特征图形的面积之和为 .
科目:初中数学 来源: 题型:
【题目】 我们定义:如图1、图2、图3,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB'C′是△ABC的“旋补三角形”,△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”.
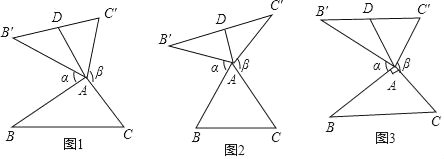
(1)①如图2,当△ABC为等边三角形时,“旋补中线”AD与BC的数量关系为:AD= BC;
②如图3,当∠BAC=90°,BC=8时,则“旋补中线”AD长为 .
(2)在图1中,当△ABC为任意三角形时,猜想“旋补中线”AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
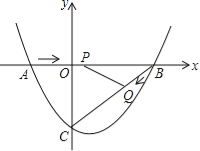
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了加大“退耕还林”的力度,出台了一系列的激励措施:在“退耕还林”过程中,每一年的林地面积达到10亩且每年的林地面积在增加的农户,当年都可得生活补贴费2000元,且每超过10亩的部分还给予奖励每亩a元,在林间还有套种其他农作物,平均每亩还有b元的收入.
下表是某农户在头两年通过“退耕还林”每年获得的总收入情况:

(注:年总收入=生活补贴量+政府奖励量+种农作物收入)
(1)试根据以上提供的资料确定a、b的值.
(2)从2003年起,如果该农户每年新增林地的亩数比前一年按相同的增长率增长,那么2005年该农户获得的总收入达到多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为边
为边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 运动到点
运动到点![]() 停止,同时点
停止,同时点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿折线
个单位长度的速度沿折线![]() 运动到点
运动到点![]() 停止,当点
停止,当点![]() 停止运动时,点
停止运动时,点![]() 也停止运动.当点
也停止运动.当点![]() 不与
不与![]() 的顶点重合时,过点
的顶点重合时,过点![]() 作
作![]() 交
交![]() 的边于点
的边于点![]() 以
以![]() 和
和![]() 为边作
为边作![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒),
(秒),![]() 的面积为
的面积为![]() (平方单位).
(平方单位).
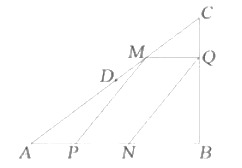
(1)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)连结![]() 直接写出
直接写出![]() 将
将![]() 分成面积相等的两部分时
分成面积相等的两部分时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).
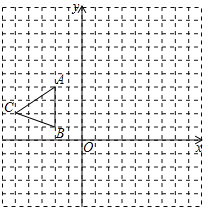
(1)请画出△ABC关于x轴对称的△A1B1C1;
(2)将△A1B1C1的三个顶点的横坐标与纵坐标同时乘-2,得到对应的点A2,B2,C2,请画出△A2B2C2;
(3)△A1B1C1与△A2B2C2面积之比为 (不写解答过程,直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答年新型冠状病毒防治全国统一考试全国卷试卷满分![]() 分,社区管理员随机从有
分,社区管理员随机从有![]() 人的某小区抽取
人的某小区抽取![]() 名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
名人员的答卷成绩,根据他们的成绩数据绘制了如下的表格和统计图:
等级 | 成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
| |
根据上面提供的信息,回答下列问题: .
(1)统计表中的![]() ,
,![]() ,
,![]() ;
;
(2)请补全条形统计图;
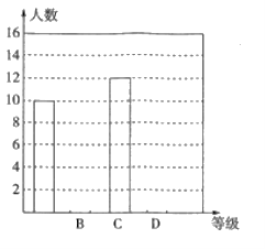
(3)根据抽样调查结果,请估计该小区答题成绩为“![]() 级”的有多少人?
级”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是⊙O的直径,BA=BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
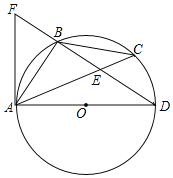
(1)求证:AF是⊙O的切线;
(2)若BC=2![]() ,BE=4,求⊙O半径r.
,BE=4,求⊙O半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“首届中国西部房.车生活文化节”期间,某汽车经销商推出![]() 四种型号的小轿车共
四种型号的小轿车共![]() 辆进行展销.
辆进行展销.![]() 型号轿车销售的成交率为
型号轿车销售的成交率为![]() ,其它型号轿车的参展轿车数的百分比与销售情况绘制如图1和如图2两幅尚不完整的统计图中.下列说法错误的是( )
,其它型号轿车的参展轿车数的百分比与销售情况绘制如图1和如图2两幅尚不完整的统计图中.下列说法错误的是( )
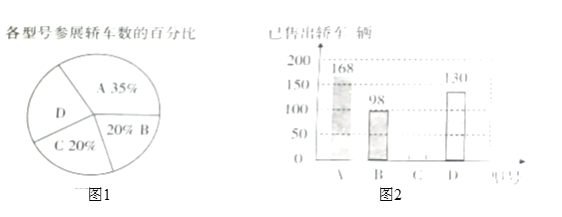
A.参加展销的![]() 型号轿车有
型号轿车有![]() 辆B.
辆B.![]() 型号轿车销售了
型号轿车销售了![]() 辆C.
辆C.![]() 型号的轿车的成交率为
型号的轿车的成交率为![]() D.
D.![]() 种型号的轿车销售情况最好
种型号的轿车销售情况最好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com