
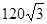 米.
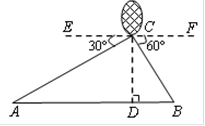
米.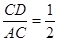 ,即可求得CD=90米.(2)在Rt△ACD中,根据正切函数的定义tan∠A=
,即可求得CD=90米.(2)在Rt△ACD中,根据正切函数的定义tan∠A=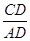 ,可求出AD的长度,同理在Rt△BCD中,根据正切函数定义tan∠B=
,可求出AD的长度,同理在Rt△BCD中,根据正切函数定义tan∠B=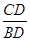 ,可求出BD的长度,从而可求出AB的长度.归纳:遇到解直角三角形的问题时,通常把要求的线段或角放在直角三角形中,利用三角函数的定义来求,如果没有直角三角形,可通过添加辅助线,构造直角三角形.
,可求出BD的长度,从而可求出AB的长度.归纳:遇到解直角三角形的问题时,通常把要求的线段或角放在直角三角形中,利用三角函数的定义来求,如果没有直角三角形,可通过添加辅助线,构造直角三角形.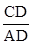 =
=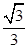 ,
,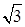 CD=90
CD=90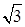 ,同理,BD=
,同理,BD=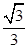 CD=30
CD=30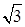 ,
,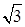 (米)
(米)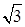 米.
米. 

科目:初中数学 来源:不详 题型:解答题
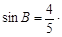
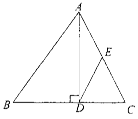
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A.100 m m | B.50 m m | C.50 m m | D. m m |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是 米,则小树AB的高是 米.
米,则小树AB的高是 米.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
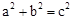 ,那么下列结
,那么下列结
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com