
【题目】某公司需要购买甲、乙两种商品共150件,甲、乙两种商品的价格分别为600元和1000元![]() 且要求乙种商品的件数不少于甲种商品件数的2倍
且要求乙种商品的件数不少于甲种商品件数的2倍![]() 设购买甲种商品x件,购买两种商品共花费y元.
设购买甲种商品x件,购买两种商品共花费y元.
![]() 请求出y与x的函数关系式及x的取值范围.
请求出y与x的函数关系式及x的取值范围.
![]() 试利用函数的性质说明,当购买多少件甲种商品时,所需要的费用最少?
试利用函数的性质说明,当购买多少件甲种商品时,所需要的费用最少?
【答案】(1)y=-400x+150000(0≤x≤50);(2)购买50件甲种商品时,所需要的费用最少.
【解析】
(1)设甲商品有x件,则乙商品则有(150-x)件,根据甲、乙两种商品共150件和乙种商品的件数不少于甲种商品件数的2倍,列出不等式组,求出x的取值范围,再根据甲、乙两种商品的价格列出一次函数关系式即可;
(2)根据(1)得出一次函数y随x的增大而减少,即可得出当x=50时,所需要的费用最少.
解:![]() 设甲商品有x件,则乙商品则有
设甲商品有x件,则乙商品则有![]() 件,根据题意得:
件,根据题意得:
![]()
解得:![]() .
.
则y与x的函数关系式是:![]() ;
;
(2)![]()
![]() 一次函数y随x的增大而减少,
一次函数y随x的增大而减少,
![]() 当
当![]() 时,
时, ![]() (元)
(元)
答:购买50件甲种商品时,所需要的费用最少.


科目:初中数学 来源: 题型:
【题目】阅读型综合题
对于实数![]() 我们定义一种新运算
我们定义一种新运算![]() (其中
(其中![]() 均为非零常数),等式右边是通常的 四则运算,由这种运算得到的数我们称之为线性数,记为
均为非零常数),等式右边是通常的 四则运算,由这种运算得到的数我们称之为线性数,记为![]() ,其中
,其中![]() 叫做线性数的一个数对.若实数
叫做线性数的一个数对.若实数 ![]() 都取正整数,我们称这样的线性数为正格线性数,这时的
都取正整数,我们称这样的线性数为正格线性数,这时的![]() 叫做正格线性数的正格数对.
叫做正格线性数的正格数对.
(1)若![]() ,则
,则![]() ,
,![]() ;
;
(2)已知![]() ,
,![]() .若正格线性数
.若正格线性数![]() ,(其中
,(其中![]() 为整数),问是否有满足这样条件的正格数对?若有,请找出;若没有,请说明理由.
为整数),问是否有满足这样条件的正格数对?若有,请找出;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元![]() 与上网时间x(h)的函数关系如图所示,则下列判断错误的是
与上网时间x(h)的函数关系如图所示,则下列判断错误的是![]()
![]()
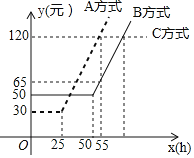
A. 每月上网时间不足25h时,选择A方式最省钱 B. 每月上网费用为60元时,B方式可上网的时间比A方式多
C. 每月上网时间为35h时,选择B方式最省钱 D. 每月上网时间超过70h时,选择C方式最省钱
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有射线AP和点B,C,请用尺规按下列要求作图:
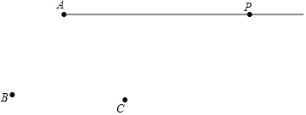
(1)连接AB,并在射线AP上截取AD=AB;
(2)连接BC、BD,并延长BC到E,使BE=BD.
(3)在(2)的基础上,取BE中点F,若BD=6,BC=4,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】窗户的形状如图所示(图中长度单位:cm),其中上部是半圆形,下部是边长相同的四个小正方形. 已知下部小正方形的边长是acm.
(1)计算窗户的面积(计算结果保留π).
(2)计算窗户的外框的总长(计算结果保留π).
(3)安装一种普通合金材料的窗户单价是175元/平方米,当a=50cm时,请你帮助计算这个窗户安装这种材料的费用(π≈3.14,窗户面积精确到0.1).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年9月1日,长春首届航空开放日在长春大房身机场正式举行,空军八一飞行表演队的新换装歼-10飞机,进行了精彩的特技飞行表演,其中一架飞机起飞0.5千米后的高度变化如下表:
高度变化 | 上升4.2 | 下降3.5 | 上升1.4 | 下降1.2 |
记作 | +4.2 | -3.5 | +1.4 | -1.2 |
(1)此时这架飞机飞离地面的高度是多少千米?
(2)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.6干米,下降2.8千米,再上升1.5千米,最后下降0.9千米.若飞机平均上升1干米需消耗6升燃油,平均下降1千米需消耗4升燃油,那么这架飞机在这4个特技表演过程中,一共消耗了多少升燃油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们都知道,![]() 表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理
表示4与-2的差的绝对值,实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离,同理![]() 也可理解为
也可理解为![]() 与3两数在数轴上所对应的两点之间的距离,
与3两数在数轴上所对应的两点之间的距离,![]() 就表示
就表示![]() 在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
在数轴上对应的点到-1的距离,由上面绝对值的几何意义,解答下列问题:
(1)求![]() .
.
(2)若![]() ,则
,则![]() .
.
(3)请你找出所有符合条件的整数![]() ,使得
,使得![]() .
.
(4)求![]() 的最小值,并写出此时
的最小值,并写出此时![]() 的取值情况.
的取值情况.
(5)已知![]() ,求
,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2﹣2ab+b.
如:2☆(﹣3)=2×(﹣3)2﹣2×2×(﹣3)+(﹣3)=27
(1)求(﹣4)☆7的值;
(2)若(1﹣3x)☆(﹣4)=32,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com