
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1、P2、P3、P4、P5是△DEF边上的5个格点,请按要求完成下列各题:
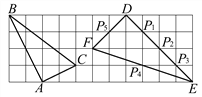
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)直接写出一个与△ABC相似的三角形,使它的三个顶点为P1、P2、P3、P4、P5中的三个格点.
【答案】(1)证明见解析(2)证明见解析(3)△P2P4P5
【解析】试题分析:(1)运用勾股定理可以得到各边的长,通过勾股定理的逆定理来证明是直角三角形.
(2)根据勾股定理求出△ABC和△DEF的各边长,然后根据“三边对应成比例的两个三角形相似”说明即可;
(3)根据△ABC的三边关系,求出点P2,P4,P5所形成三角形的三边长,根据“三边对应成比例的两个三角形相似”解答即可,
解:(1)根据勾股定理,
得AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]() ;
;
∴AB2+AC2=BC2,
∴△ABC 为直角三角形
(2)△ABC和△DEF相似.理由如下:
∵AB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
DE=![]() ,DF=
,DF=![]() ,EF=
,EF=![]() .
.
∴![]() ,
,
∴△ABC∽△DEF
(3连接P2P5,P2P4,P4P5.

∵P2P5=![]() ,P2P4=
,P2P4=![]() ,P4P5=
,P4P5=![]() ,AB=
,AB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴![]() ,
,
∴△ABC∽△P4P5P2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】补全解答过程:
已知:如图,直线AB∥CD,直线EF与直线AB,CD分别交于点G,H;GM平分∠FGB,∠3=60°.求∠1的度数.
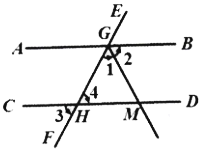
解:∵EF与CD交于点H,(已知)
∴∠3=∠4.( )
∵∠3=60°,(已知)
∴∠4=60°.( )
∵AB∥CD,EF与AB,CD交于点G,H,(已知)
∴∠4+∠FGB=180°.( )
∴∠FGB= .
∵GM平分∠FGB,(已知)
∴∠1= °.(角平分线的定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
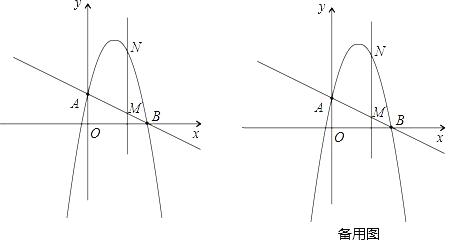
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,A点表示2,现在点A向右移动两个单位后到达点B;再向左移动10个单位到达C点:
(1)请在数轴上表示出A点开始移动时位置及B、C点位置;
(2)当A点移动到C点时,若要再移动到原点,问必须向哪个方向移动多少个单位?
(3)请把A点从开始移动直至到达原点这一过程,用一个有理数算式表达出来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com