练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．计算$\frac{2}{x-1}$+$\frac{3}{1-x}$的结果是$\frac{1}{1-x}$．

    分析 先将分式通分，再按照分式的运算法则进行运算即可得出结论．

    解答 解：原式=-$\frac{2}{1-x}$+$\frac{3}{1-x}$=$\frac{1}{1-x}$．
    故答案为：$\frac{1}{1-x}$．

    点评 本题考查了分式的加减法，解题的关键是将分式进行通分．本题属于基础题，难度不大，解决该题型题目时，将分式进行化简是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．已知关于x，y的二元一次方程组$\left\{\begin{array}{l}{2x-y=2}\\{ax+5y=29}\end{array}\right.$与$\left\{\begin{array}{l}{x-2y=-5}\\{4x+by=40}\end{array}\right.$的解相同，求a，b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如果不等式（a-1）x＞b的解集是x＜$\frac{b}{a-1}$，则a的取值范围是a＜1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图甲，平行四边形ABCD外有一条直线MN，过A、B、C、D4个顶点分别作MN的垂线AA1、BB1、CCl、DDl，垂足分别为Al、B1、Cl、D1．
    （1）求证：AA1+CCl=BB1+DDl；
    （2）如图乙，直线MN向上移动，使点A与点B、C、D位于直线MN两侧，这时过A、B、C、D向直线MN引垂线，垂足分别为Al、B1、Cl、D1，那么AA1、BB1、CCl、DDl之间存在什么关系？
    （3）如图丙，如果将MN再向上移动，使其两侧各有2个顶点，这时过A、B、C、D向直线MN引垂线，垂足分别为Al、B1、Cl、D1，那么AA1、BB1、CCl、DD1之间又存在什么关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

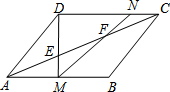    10．平行四边形ABCD中，AB=28，E、F是对角线AC上的两点，且AE=EF=FC，DE交AB于点M，MF交CD于点N．求AM、CN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

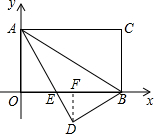    20．如图所示，已知：把矩形AOBC放入直角坐标系xOy中，使OB、OA分别落在x轴、y轴上，点C的坐标为（8，4），将△ABC沿AB翻折，使C点落在该坐标平面内的D点处，AD交x轴于点E．
    （1）求D点坐标；
    （2）求直线AD的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．反比例函数y=（4-3k）${x}^{{k}^{2}-5k-1}$，当x＞0时，y随x的增大而减小，则k=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

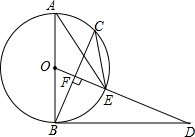    4．如图，AB是⊙O的直径，BD是⊙O的切线，点C为⊙O上一点，0D⊥BC于点F交⊙O于点E，连接AE、C′E．
    （I）求证：∠ODB=∠AEC；
    （2）若⊙O的半径为4，sinA=$\frac{3}{4}$，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

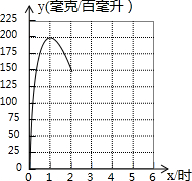    5．某医药研究所开发一种新药，实验数据显示，如果成人按规定的剂量服药，1.5小时内血液中含药量y1（毫克/百毫升）与时间x（时）的关系可以近似地用二次函数刻画（0≤x＜1.5），服药后1小时，血液中含药量达到最高值200毫克/百毫升，1.5小时后（包含1.5小时），经过凋查，测得如下数据：
     x 1.52.5 3 4.5  5…
     y 150 90 75 5045 …
    （1）求出1.5小时内血液中含药量y1与时间x之间的函数关系式．
    （2）在坐标系中描出上述表格中各点，猜想并求出1.5小时后血液中含药量y2与时间x所满足的函数关系式．
    （3）当血液中的含药量大于或等于72毫克/百毫升时属于“治疗最佳期”，请问：服药后哪一段时间属于“治疗最佳期”？
    （4）当血液中的含药量大于或等于30毫克/百毫升时属于“治疗有效期”，假设某病人晚上20：00服药，第二天早上7：00时是否应该再一次服药，请说明理由．

    查看答案和解析>>

    同步练习册答案