
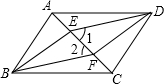
 (1)如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF.求证:∠1=∠2.
(1)如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF.求证:∠1=∠2.分析 (1)根据平行四边形的对边平行且相等,得AB=CD,AB∥CD,再根据平行线的性质,得∠BAE=∠DCF,∠AEB=∠CFD,由AAS证明△ABE≌△CDF,根据全等三角形的对应边相等,得BE=DF,从而得出四边形BFDE是平行四边形,根据两直线平行内错角相等证得∠1=∠2;
(2)根据y与x+2成正比例关系设出函数的解析式,再把当x=1时,y=-6代入函数解析式即可求出k的值,进而求出y与x之间的函数解析式.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠BAE=∠DCF,
∵BE∥DF,
∴∠BEF=∠EFD,
又∠BEF+∠AEB=180°,
∠EFD+∠DFC=180°,
∴∠AEB=∠CFD,
在△ABE与△CDF中,$\left\{\begin{array}{l}{∠AEB=∠CFD}\\{∠BAE=∠DCF}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△CDF,
∴BE=DF,
又BE∥DF,
∴四边形BFDE是平行四边形,
∴DE∥BF,
∴∠1=∠2;
(2)解:∵y与x+2成正比例
∴可设y=k(x+2),把当x=1时,y=-6.代入得-6=k(1+2).
解得:k=-2.
故y与x的函数关系式为y=-2x-4.
点评 本题考查的是利用平行四边形的性质,全等三角形的判定与性质,待定系数法求一次函数解析式,以及一次函数图象上点的坐标特征,熟练掌握待定系数法是解本题的关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{2}$=$\frac{3}{b}$ | B. | $\frac{a}{3}$=$\frac{b}{2}$ | C. | $\frac{a}{b}$=$\frac{2}{3}$ | D. | $\frac{b}{a}$=$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
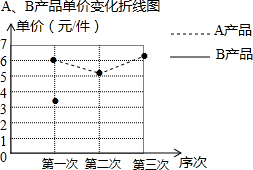 某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.
某厂生产A,B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了单价变化不完整的统计表及折线图.| 第一次 | 第二次 | 第三次 | |
| A产品单价(元/件) | 6 | 5.2 | 6.5 |
| B产品单价(元/件) | 3.5 | 4 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
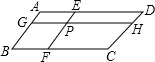 如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.
如图,在平行四边形ABCD中,过点P作直线EF、GH分别平行于AB、BC,那么图中共有( )平行四边形.| A. | 4个 | B. | 5个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=6}\\{x=3y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=6}\\{y=3x}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=6}\\{x=3y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2x+y=6}\\{y=3x}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 6个 | C. | 12个 | D. | 16个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com