
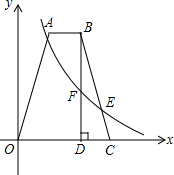
 如图,在四边形OABC中,AB∥OC,OA=BC,点B,C的坐标分别为(4,8),(6,0),E为BC上一点,且BE=3CE,过点B作BD⊥x轴于点D.双曲线y=$\frac{k}{x}$(x>0)经过点E,且交BD于点F.
如图,在四边形OABC中,AB∥OC,OA=BC,点B,C的坐标分别为(4,8),(6,0),E为BC上一点,且BE=3CE,过点B作BD⊥x轴于点D.双曲线y=$\frac{k}{x}$(x>0)经过点E,且交BD于点F.分析 (1)过E作EH⊥OC于H,设E(m,$\frac{k}{m}$),由已知条件得到CH=6-m,根据EH∥BD,得到$\frac{CH}{CD}=\frac{CE}{BC}$=$\frac{EH}{8}$,求得E($\frac{11}{2}$,2),由于双曲线y=$\frac{k}{x}$(x>0)经过点E,于是得到k=11,由OD=4,得到点F的横坐标为4,即可得到F(4,$\frac{11}{4}$);
(2)根据等腰梯形的面积公式即可得到结论.
解答 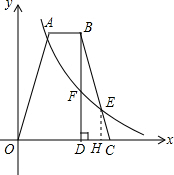 解:(1)∵点B,C的坐标分别为(4,8),(6,0),
解:(1)∵点B,C的坐标分别为(4,8),(6,0),
∴BD=8,OD=4,OC=6,
∴CD=2,BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=2$\sqrt{17}$,
过E作EH⊥OC于H,
设E(m,$\frac{k}{m}$),则CH=6-m,
∵BD⊥OC,
∴EH∥BD,
∴$\frac{CH}{CD}=\frac{CE}{BC}$=$\frac{EH}{8}$,
即$\frac{6-m}{2}=\frac{1}{4}$,
∴m=$\frac{11}{2}$,EH=2,
∴E($\frac{11}{2}$,2),
∵双曲线y=$\frac{k}{x}$(x>0)经过点E,
∴k=11,
∵OD=4,
∴点F的横坐标为4,
∴DF=$\frac{11}{4}$,
∴F(4,$\frac{11}{4}$);
(2)∵四边形OABC是等腰梯形,
∴AB=OC-2CD=2,
∴S四边形OABC=$\frac{1}{2}$(2+6)×8=32.
点评 本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特点,等腰梯形的面积的计算,平行线分线段成比例定理,掌握的作出辅助线是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 摸出的三个球中至少有两个球是黑球 | |
| B. | 摸出的三个球中至少有两个球是白球 | |
| C. | 摸出的三个球中至少有一个球是黑球 | |
| D. | 摸出的三个球中至少有一个球是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是6π-9$\sqrt{3}$.
如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是6π-9$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-1)-2=x2 | B. | x2n÷x2=xn(n是正整数) | ||
| C. | (-2x2)3=-6x6 | D. | (-3a-2)(3a-2)=9a2-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com