
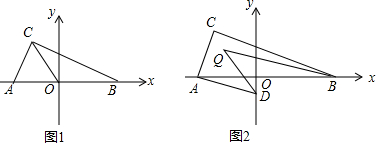
分析 (1)根据非负性求出a,b的值;
(2)根据三角形的面积建立方程求出点M的坐标;
(3)利用平行线的性质,和整体思想求出角的度数.
解答 解:(1)∵|2a+b+1|+(a+2b-4)2=0,
∴2a+b+1=0,a+2b-4=0,
∴a=-2,b=3,
(2)由(1)有a=-2,b=3,
∴A(-2,0),B(3,0),
∴AB=5,
∴S△ABC=$\frac{1}{2}$AB×|yC|=$\frac{1}{2}$×5×2=5,
∵△COM的面积是△ABC的面积的一半,
∴S△COM=$\frac{5}{2}$,
①当点M在x轴上时,设M(m,0),
∴S△COM=$\frac{1}{2}$×OM×|yC|=$\frac{1}{2}$×|m|×2=$\frac{5}{2}$,
∴|m|=$\frac{5}{2}$,∴m=±$\frac{5}{2}$,
∴M(-$\frac{5}{2}$,0)或M($\frac{5}{2}$,O),
②当点M在y轴上时,
设M(0,n)
∴S△COM=$\frac{1}{2}$×OM×|xC|=$\frac{1}{2}$×|n|×1=$\frac{5}{2}$,
∴|n|=5,
∴n=±5,
∴M(0,-5)或M(0,5),
(3)过点Q作∥BC,
∴QM∥BC∥AD,
∴∠DQB=∠CBQ+∠ADQ=45°
点评 此题是坐标与图形题,主要考查绝对值和平方的非负性,三角形面积的应用,角的计算,解本题的关键是求出△ABC的面积.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
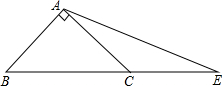 己知,△ABC中,AB=AC=1,∠BAC=90°,P是BC延长线上的动点,∠PAC=α.
己知,△ABC中,AB=AC=1,∠BAC=90°,P是BC延长线上的动点,∠PAC=α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
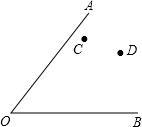 如图所示,点C、D是∠AOB内部的两点.
如图所示,点C、D是∠AOB内部的两点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com